 |
 |
Abstract
Linkage disequilibrium (LD) plays an important role in genomic selection and mapping quantitative trait loci (QTL). In this study, the pattern of LD and effective population size (Ne) were investigated in Chinese beef Simmental cattle. A total of 640 bulls were genotyped with IlluminaBovinSNP50BeadChip and IlluminaBovinHDBeadChip. We estimated LD for each autosomal chromosome at the distance between two random SNPs of <0 to 25 kb, 25 to 50 kb, 50 to 100 kb, 100 to 500 kb, 0.5 to 1 Mb, 1 to 5 Mb and 5 to 10 Mb. The mean values of r2 were 0.30, 0.16 and 0.08, when the separation between SNPs ranged from 0 to 25 kb to 50 to 100 kb and then to 0.5 to 1 Mb, respectively. The LD estimates decreased as the distance increased in SNP pairs, and increased with the increase of minor allelic frequency (MAF) and with the decrease of sample sizes. Estimates of effective population size for Chinese beef Simmental cattle decreased in the past generations and Ne was 73 at five generations ago.
Linkage disequilibrium (LD) denotes non-random association between alleles at different loci. LD is the theoretical basis of genomic selection (GS) and genome-wide association study (GWAS), that is also important in gene mapping, estimates for effective population size, population structure and so on (Nachman, 2002). Molecular markers such as single nucleotide polymorphisms (SNPs) and microsatellites were widely used to estimate the extent of LD. The level of LD is usually influenced by non-genetic factors and genetic factors containing genetic linkage, selection, the rate of recombination, the rate of mutation, genetic drift, non-random mating and population structure.
The effective population size (Ne) is defined as the number of individuals in an ideal population that would show the same amount of dispersion of allele frequencies under random genetic drift or the amount of inbreeding as in the population under consideration, and is usually less than the absolute population size (Wright, 1938). Ne is an important parameter, as it can help to explain how cattle populations evolve and expand, and by definition describe the rate of inbreeding accumulation and loss of genetic variation. Estimates for Ne can be obtained from heterozygote excess or LD. Presently, estimates for Ne based LD data are are more frequently used than heterozygote excess, and therefore complement evolutionary studies of cattle populations (Hayes et al., 2003).
Recently the discovery of large numbers of SNP through sequencing of the cattle genome has generated extensive research in quantifying LD characteristics (Farnir et al., 2000; Odani et al., 2006; McKay et al., 2007; Sargolzaei et al., 2008; Kim and Kirkpatrick, 2009; Qanbari et al., 2010). A recent report showed that high density markers were used to study the extent of LD in Angus, Charolais and Crossbred beef cattle (Lu et al., 2012). However, similar studies were not reported in Simmental cattle which are an important economic breed of beef cattle. LD indicates population characteristics and has different pattern on each chromosome. Hence, it is necessary to study the extent of LD, and then to estimate effective population size in Simmental cattle.
China’s role in international beef markets has grown significantly in the past years, and domestic production is projected to continue to increase (Longworth et al., 2001). However, China does not have special-purpose beef cattle. To increase beef production, American, Canadian and Australian Simmental cattle have been introduced into China and crossbred with native dual-purpose Simmental cattle, which are named Chinese beef Simmental cattle. In current research, high density SNPs data from Chinese beef Simmental cattle were used to analyze the pattern of LD, and to infer the effective population size up to 2000 generations ago. Meanwhile, we evaluated the effects of minor allelic frequency (MAF) and sample size on LD estimations.
Experimental animals consisted of 640 young Simmental bulls, born in 2008 to 2010, originated from Ulgai, located at Xilingol league, Inner Mongolia, China. DNA was extracted from blood of the bulls using the routine procedures. The IlluminaBovineHD chip was used to genotype 504 young bulls and their autosomal chromosomes contained total of 735,293 SNPs. Additionally, 136 young bulls were genotyped with IlluminaBovineSNP50, and 51,582 SNPs were detected on their autosomal chromosomes. There were 46,000 SNPs in common between two chips. In the present study, quality control standards for SNPs data were Hardy-Weinberg equilibrium (p>10−3), MAF>0.05, SNP call rate >0.95 and Mendel error rate <0.05. 35,079 common SNPs survived after being filtered on quality control standards, which were used to analyze the extent of LD.
Several statistics parameters were proposed to measure the extent of LD. D′ (Lewontin, 1964) and r2 (Hill, 1974) were widely used in practice, but their functions are different. r2 was considered to be a better descriptor of LD as it is more robust and not sensitive to changing gene frequency and effective population size (Terwilliger et al., 2002; Zhao et al., 2007).
Assume two loci A and B, each locus has two alleles (denoted A1, A2 and B1, B2, respectively). PA1, PA2, PB1 and PB2 are the frequency of each of the alleles. P11, P12, P21 and P22 show the frequency of haplotypes A1B1, A1B2, A2B1 and A2B2. Thus, r2 can be expressed as:
PLINK (Purcell et al., 2007) includes a set of options to calculate pair-wise linkage disequilibrium between SNPs, and to present or process this information in various ways. In this study, we used the command plink -cow -bfile filename -ld-window-r2 0 -out outname. To display the decay of LD, distances of pair-wise SNPs were binned into seven types of intervals (0 to 25 kb, 25 to 50 kb, 50 to 100 kb, 100 to 500 kb, 0.5 to 1 Mb, 1 to 5 Mb and 5 to 10 Mb) along the first 10 Mb of each chromosome, and mean r2 was computed for each interval. Table 2 shows information for all the SNP pair groups.
Three factors, chromosomes, MAF and sample sizes, affecting LD estimation were studied based on r2 data computed above.
In the high-density SNP chip, genetic distance for SNP pairs could not be obtained. Therefore, physical distance was used to replace genetic distance for the estimation of effective population size in the current study. l00 kb of physical distance in genetic distance is approximate equivalent to 0.1 cM. SNP physical position from the UMD 3.1 bovine assembly (http://www.ncbi.nlm.nih.gov/assembly/313678/) was used in this study.
LD data make it feasible to estimate Ne. Sved (1971) has proposed the relationship formula for LD and Ne as follows:
Where Ne is the effective population size, r2 is the mean value of LD estimation value of SNP pairs. k is 4 or 2, which denotes autosomal chromosomes or sex chromosomes respectively. c represents the genetic distance in Morgan (M). Generation is calculated with 1/2c. n is the chromosome experimental sample size. α = 1 (Sved, 1971) in the absence of mutation, otherwise α = 2 (Lewontin, 1964; Weir and Hill, 1980; McVean, 2002). In the majority of studies, the formula for the absence of mutation is chosen to estimate Ne. Hence, in our study, k = 4 and c = 1 were chosen. Seven types of SNP pairs with the physical distances 25 kb, 50 kb, 100 kb, 500 kb, 1 Mb, 5 Mb and 10 Mb were respectively chosen to estimate the Ne of Chinese beef Simmental cattle from 5 generations ago.
SNPs information for every autosomal chromosome is given in Table 1. The total autosomal chromosome length of Chinese beef Simmental cattle was 2,541.30 Mb. The longest Bos taurus autosomal chromosome is BTA1 (length = 158.14 Mb), and the shortest is BTA25 (length = 42.80 Mb). 35,079 common SNPs between two chips covered the whole genome in this study. Average adjacent SNPs spacing was 54.17±61.44 kb, and the largest spacing situated on BTA14 was 3620 kb (between ARS-BFGL-NGS-37733 and Hapmap42739-BTA-95927). The mean MAF of the genome was 0.28±0.13, and followed an almost uniform distribution, as can be seen in Figure 1.
The mean values of r2 for each autosomal chromosome for distance bins of 0 to 25 kb, 25 to 50 kb, 50 to 100 kb, 100 to 500 kb, 0.5 to 1 Mb, 1 to 5 Mb and 5 to 10 Mb were calculated. Table 2 shows that the average r2 is 0.30, 0.23, 0.16, 0.08, 0.05, 0.04 and 0.03 at different distance bins for Simmental cattle, respectively. Figure 2 shows the LD decay over varying distances of the genome. The measured LD was high for pairs of SNPs within close proximity. However, there is a strong LD in the long distance SNP pairs.
The extent of LD was significantly different among chromosomes. The average r2 for SNPs separated by intervals 0 to 25 kb, 25 to 50 kb, 50 to 100 kb, 100 to 500 kb, 0.5 to 1 Mb, 1 to 5 Mb and 5 to 10 Mb in each autosomal chromosome are presented in Table 3. The mean value of r2 for distances less than 25 kb was 0.30, but higher for BTA9 and BTA21 (0.363 and 0.364, respectively), and lower for BTA27 (0.209). The average of r2 was 0.30 in SNP pairs with physical distances of <25 kb and decreased to 0.16 at distances of 50 to 100 kb, this result was similar to that previously reported (Qanbari et al., 2010; Lu et al., 2012). A similar study found the extent of LD (r2 = 0.59) in approximately 50 kb on north American Holstein cattle, which was much larger than that found in our study (Sargolzaei et al., 2008).
In this study, three different minimum allelic frequency (MAF) thresholds (0.05, 0.1 and 0.2) were used to study the effects of MAF on the extent of LD. Figure 3 shows that MAF has a significantly effect on the mean value of r2, especially over short distances (0 to 25 kb). The mean values of r2 increase significantly with an increasing MAF. For example, from 0 to 25 kb, the mean value of r2 for MAF≥0.05 was 0.24, however, with MAF≥0.1 and 0.2, the mean value of r2 increased to 0.29 and 0.34, respectively.
As can be seen in Figure 4, sample sizes affect the LD estimation value. In this paper, five different sample sizes of n = 25, n = 50, n = 100, n = 200 and n = 400 were randomly selected from the total set to study the effect of sample size on estimates of the level of LD. The mean r2 were greater when sample size is smaller, and this phenomenon is more noticeable for LD estimation across a SNP interval more than 500 kb. There were no significant differences for LD estimates when sample sizes were greater than 400 and SNP distances less than 50 kb.
The extent of LD for different chromosome fragment length could reflect the effective population size of different past generations. Table 4 shows Ne of Simmental cattle in past generations. Estimates of Ne for 2,000 generations ago was approximately 2,377 and down to 73 at 5 generations ago. Estimates of Ne for Chinese beef Simmental cattle show an increasing trend when plotted against increasing past generations (Figure 5).
Recent developments in high-throughput SNP panels have generated enthusiasm and interesting in GS and GWAS on cattle. Linkage disequilibrium maps can increase power and precision in association mapping. Qanbari et al. (2010) reported an average level LD of 0.30 over pair wise distances less than 25 kb based on 40,854 SNPs in 810 German Holstein cattle. Kim and Kirkpatrick (2009) reported LD of >0.80 over genomic regions of approximately 50 kb using 7119 SNPs in North America Holstein cattle. Lu et al. (2012) reported the extent of LD in Angus, Charolais and crossbred beef cattle based on Illumina BovineSNP50_v2 Beadchip and Illumina BovineSNP50_v1 Beadchip, with the level of LD being 0.29, 0.22 and 0.15 when the distance range between markers is 0 to 30 kb, respectively. This could be attributed in part to the difference in populations between the current study and previously reported research. Furthermore, in the current study, we used 35,079 SNPs distributed across the entire bovine autosomal chromosome for the analysis of LD in Chinese beef Simmental cattle. The r2 statistic denotes the extent of LD. The extent of LD showed a decreasing tendency with increasing distances of the genome. The mean r2 was much higher between close loci, and the result was the same as previously reported estimates (Farnir et al., 2000; Smith et al., 2006; Kim and Kirkpatrick, 2009; Qanbari et al., 2010; Lu et al., 2012). However, a low level of LD can exist between two SNPs that are closely adjacent, while markers that are more distant can show a higher than expected level of LD. This situation also appeared in linkage disequilibrium studies on human and model animals (Reich et al., 2001). It could be caused by selection, the rate of recombination, mutation and genetic drift (Nachman, 2002).
The mean r2 values were different for the same fragment length on different autosomal chromosomes. Higher LD was found for BTA21. This may reflect selection for traits that are strongly influenced by QTL on this chromosome in this breed. Chinese beef Simmental cattle are a popular breed in Chinese beef production and genetic trends suggest a strong selection for growth and meat traits. A majority of studies have shown highly significant evidence for the presence of QTLs affecting meat traits (McClure et al., 2010) on BTA21. In addition, when selection operates at a locus, the neighboring loci in close linkage with the locus under selection will have an enhanced extend of LD. When selection occurs at multiple loci in epistasis, LD between loci under epistatic selection and their tightly linked loci will be created and enhanced (Du et al., 2007).
Estimates of LD across the whole genome could be affected by many factors. In this study, removing SNPs with very low MAFs also lead to lower numbers of SNPs available for study, which can also lead to bias of LD estimates. There are several published papers observing a similar phenomenon in other species (Khatkar et al., 2008; Yan et al., 2009; Qanbari et al., 2010). LD estimation is greater with MAF increasing at a short SNP pairs distance, but the phenomenon is not sensitive when SNP pairs achieve a distance of 1 Mb. Sample size is another factor that affects estimation of the extent of LD (Khatkar et al., 2008; Yan et al., 2009). A small sample size (n = 25) can also lead to the biased estimates for LD. However, there are no significant differences for the mean r2 when sample sizes exceed 100, especially when the given extent interval of LD is less than 100 kb. In addition, previous research on Holstein cattle demonstrated that a sample of 400 or more was required for reliable estimation of LD (Khatkar et al., 2008). A similar study in humans that found sample sizes would be even higher, which may be due to humans having a larger effective population size (Chen et al., 2006).
Hill (1974) proposed a method for estimating effective population sizes. In this method, estimates of Ne depend on the number of animals alive at any time and the variance of progeny number per sire. In addition, previous research showed that the latter played a key role in the decrease of the population size (Mukai et al., 1989; Nomura et al., 2001). To maximize the net response in economic merit for dairy cattle, FAO (1998) reported an effective population size of 50 per generation was required to maintain the fitness in a breed. Goddard and Smith (1990) suggested a minimum effective number of 10 bull sires per generation, equivalent to 40 individuals per generation. McParland et al. (2007) used this traditional method to estimate Ne for 550,591 Ireland Simmental cattle, the result showed that Ne was 127 at the current generation. However, pedigree information was often missing or error that caused the decline of Ne estimated accuracy. In our study, the estimate for Ne of Chinese beef Simmental cattle was approximately 73 for 5 generations ago, well above the reported numbers. This could be attributed to a sufficiently large number of sires being used to produce animals in the current dataset, and thus a small variance of family size was generated. The slope of the Ne suggests that the population sizes were decreasing consistently fast, possibly due to the use of artificial selection, and therefore actions is required to maintain a larger Ne.
ACKNOWLEDGMENTS
Research was supported by the 12th “Five-Year” National Science and Technology Support Project (#2011BAD28B04), basic research fund program of state-level public welfare scientific research institutions of Institute of Animal Sciences, CAAS (#2010jc-2), the Agriculture Ministry Special Project (#CARS-38), Chinese National Programs for High Technology Research and Development (#2013AA102505-4), The Incremental Budget Program for the Fundamental Research of the Chinese Academy of Sciences (#2013ZL031), National Natural Science Foundation of China (31201782). Beijing Natural Science Foundation (6133033) and China Postdoctoral Science Foundation funded project (2012M510011).
Figure 3.
Average r2 estimates at different physical distances for three different minor allelic frequency (MAF) thresholds. Mean LD estimates are pooled over all autosomal chromosomes, and three different minimum threshold cut off levels for minimum allele frequency are shown.

Figure 4.
Average r2 estimates at different physical distances for six different sample sizes. Mean LD estimates are pooled over all chromosomes, and six different sample sizes are shown.
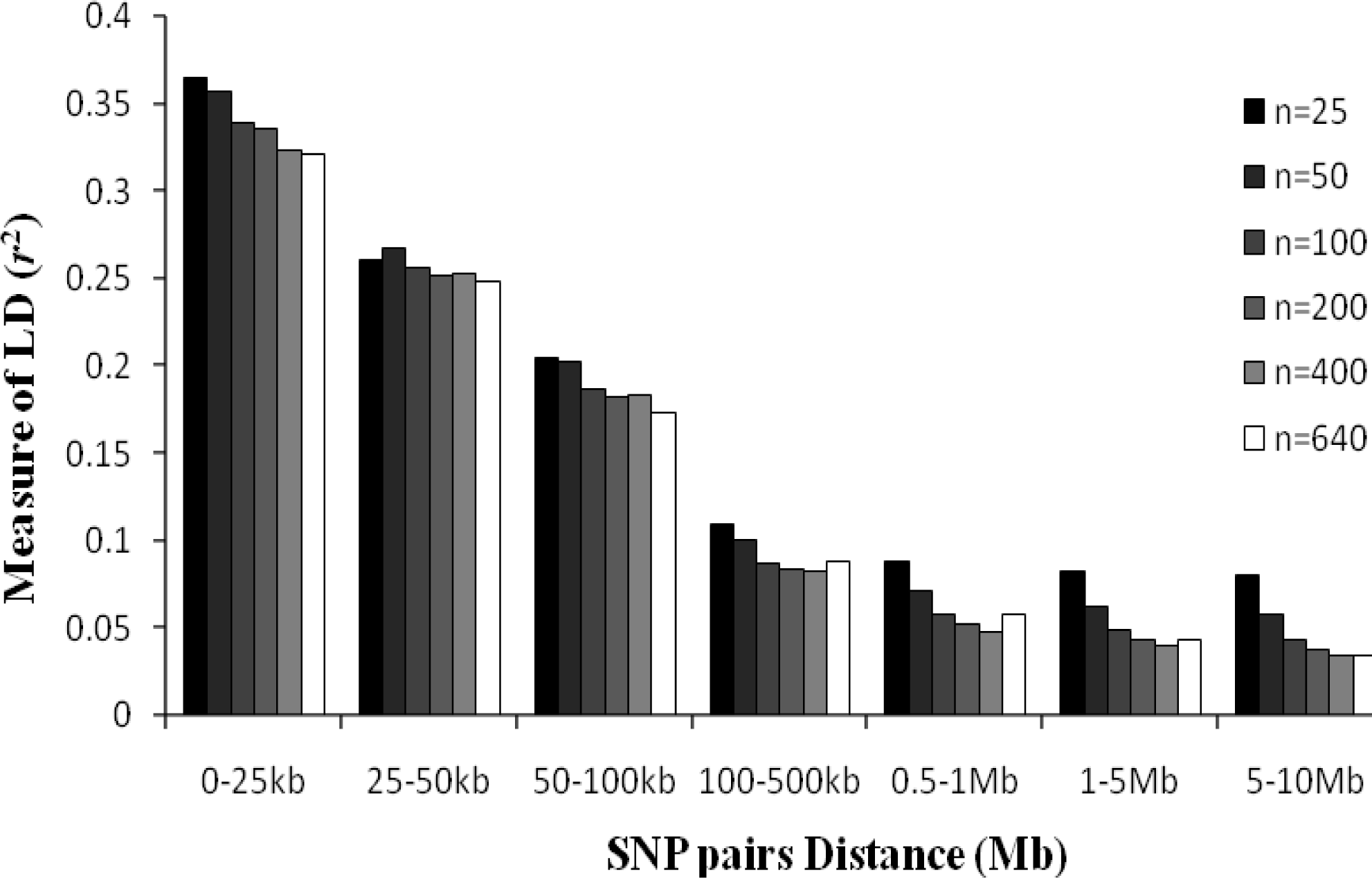
Figure 5.
Estimated Ne for Chinese beef Simmental cattle over time from linkage disequilibrium data.

Table 1.
Statistical information for analyzed SNP
Table 2.
Statistical information for LD over various distances
| Distance | Number of SNP pairs | Average r2 |
|---|---|---|
| 0–25 kb | 4,100 | 0.30 |
| 25–50 kb | 12,412 | 0.23 |
| 50–100 kb | 18,855 | 0.16 |
| 100–500 kb | 92,378 | 0.08 |
| 0.5–1 Mb | 179,984 | 0.05 |
| 1–5 Mb | 368,467 | 0.04 |
| 5–10 Mb | 654,755 | 0.03 |
Table 3.
Statistical information for average r2 as distance between pairs of SNP up to 10Mb for the genome
REFERENCES
Du FX, Clutter AC, Lohuis MM. 2007. Characterizing linkage disequilibrium in pig populations. Int J Biol Sci 3:166–178.



FAO. 1998. Secondary Guidelines for Development of National Farm Animal Genetic Resources Management Plans: Managementof Small Populations at Risk. FAO; Rome, Italy:
Farnir F, Coppieters W, Arranz JJ. 2000. Extensive genome-wide linkage disequilibrium in cattle. Genome Res 10:220–227.


Goddard MG, Smith C. 1990. Optimum number of bull sires in dairy cattle breeding. J Dairy Sci 73:1113–1122.

Hayes BJ, Visscher PM, McPartlan HC, Goddard ME. 2003. Novel multilocus measure of linkage disequilibrium to estimate past effective population size. Genome Res 13:635–643.



Hill WG. 1974. Estimation of linkage disequilibrium in randomly mating populations. Heredity 33:229–239.


Khatkar M, Nicholas F, Collins A, Zenger K, Cavanagh J, Barris W, Schnabel R, Taylor J, Raadsma H. 2008. Extent of genome-wide linkage disequilibrium in Australian Holstein-Friesian cattle based on a high-density SNP panel. BMC Genomics 9:187



Kim ES, Kirkpatrick BW. 2009. Linkage disequilibrium in the North American Holstein population. Anim Genet 40:279–288.


Lewontin RC. 1964. The interaction of selection and linkage .i. general considerations; heterotic models. Genetics 49:49–67.




Longworth JW, Brown CG, Waldron SA. 2001. Beef in China: agribusiness opportunities and challenges. University of Queensland Press.
Lu D, Sargolzaei M, Kelly M, Li C, Gordon VV, Wang Z, Plastow G, Moore S, Miller SP. 2012. Linkage disequilibrium in Angus, Charolais, and Crossbred beef cattle. Front Genet 3:152–161.



McParland S, Kearney JF, Rath M. 2007. Inbreeding trends and pedigree analysis of Irish dairy and beef cattle populations. J Anim Sci 85:322–331.


McKay S, Schnabel R, Murdoch B, Matukumalli LK, Aerts J, Coppieters W, Crews D, DiasNeto E, Gill CA, Gao C, Mannen H, Stothard P. 2007. Whole genome linkage disequilibrium maps in cattle. BMC Genet 8:74



McClure MC, Morsci NS, Schnabel RD, Kim JW, Yao P, Rolf MM, Mckay SD, Greqq SJ, Taylor JF. 2010. A genome scan for quantitative trait loci influencing carcass, post-natal growth and reproductive traits in commercial Angus cattle. Anim Genet 41:597–607.


Mukai F, Tsuj S, Fukazawa K, Ohtagaki S, Nambu Y. 1989. History and population structure of a closed strain of Japanese black cattle. J Anim Breed Genet 106:254–264.

Nachman MW. 2002. Variation in recombination rate across the genome: evidence and implications. Curr Opin Genet Dev 12:657–663.


Nomura T, Honda T, Mukai F. 2001. Inbreeding and effective population size of Japanese Black cattle. J Anim Sci 79:366–370.


Odani M, Narita A, Watanabe T, Yokouchi K, Sugimoto Y, Fujita T, Oguni T, Matsumoto M, Sasaki Y. 2006. Genome-wide linkage disequilibrium in two Japanese beef cattle breeds. Anim Genet 37:139–144.


Purcell S, Neale B, Todd-Brown K, Thomas L, Ferreira MA, Bender D, Maller J, Sklar P, Bakker PI, Daly MJ, Sham PC. 2007. PLINK: A tool set for whole-genome association and population-based linkage analyses. Am J Hum Genet 81:559–575.



Qanbari S, Pimentel ECG, Tetens J, Thaller G, Lichtner P, Sharifi AR, Simianer H. 2010. The pattern of linkage disequilibrium in German Holstein cattle. Anim Genet 41:346–356.


Reich DE, Cargill M, Bolk S, Ireland J, Sabeti PC, Richter DJ, Lavery T, Kouyoumjian R, Farhadian SF, Ward R, Lander ES. 2001. Linkage disequilibrium in the human genome. Nature 411:199–204.


Sargolzaei M, Schenkel FS, Jansen GB, Schaeffer LR. 2008. Extent of linkage disequilibrium in Holstein cattle in North America. J Dairy Sci 91:2106–2117.


Smith EM, Wang X, Littrell J, Eckert J, Cole R, Kissebah AH, Olivier M. 2006. Comparison of linkage disequilibrium patterns between the HapMap CEPH samples and a family-based cohort of Northern European descent. Genomics 88:407–414.



Sved JA. 1971. Linkage disequilibrium and homozygosity of chromosome segments in finite populations. Theor Popul Biol 2:125–141.


Terwilliger JD, Haghighi F, Hiekkalinna TS, Goring HHH. 2002. A biased assessment of the use of SNPs in human complex traits. Curr Opin Genet Dev 12:726–734.


Wright S. 1938. Size of population and breeding structure in relation to evolution. Science 87:430–431.
Weir BS, Hill WG. 1980. Effect of mating structure on variation in linkage disequilibrium. Genetics 95:477–488.




- TOOLS
-
METRICS

- Related articles
-
Linkage Disequilibrium and Effective Population Size in Hanwoo Korean Cattle2011 December;24(12)







 PDF Links
PDF Links PubReader
PubReader ePub Link
ePub Link Full text via DOI
Full text via DOI Full text via PMC
Full text via PMC Download Citation
Download Citation Print
Print




