 |
 |
| Anim Biosci > Volume 37(4); 2024 > Article |
|
Abstract
Objective
Methods
Results
Conclusion
Notes
AUTHOR CONTRIBUTIONS
Conception and design of study: JKH, YSK, HBP
Acquisition of data: JKH, YMK, ESC, YSK
Analysis and/or interpretation of data: JKH, YMK, ESC, JBL, YSK, HBP
Drafting the manuscript: JKH, HBP
Critical review/revision: JKH, YMK, YSK, HBP
Others: JKH, YMK, ESC, JBL, YSK, HBP
CONFLICT OF INTEREST
We certify that there is no conflict of interest with any financial organization regarding the material discussed in the manuscript.
FUNDING
This work was supported by the National Institute of Animal Science, Rural Development Administration, Republic of Korea and formed part of an internal project (Grant ID: PJ014289). This work also funded by the National Research Foundation of Korea grant supported by the Ministry of Education, Republic of Korea (No: 2022R111A3071786).
ACKNOWLEDGMENTS
Figure 1
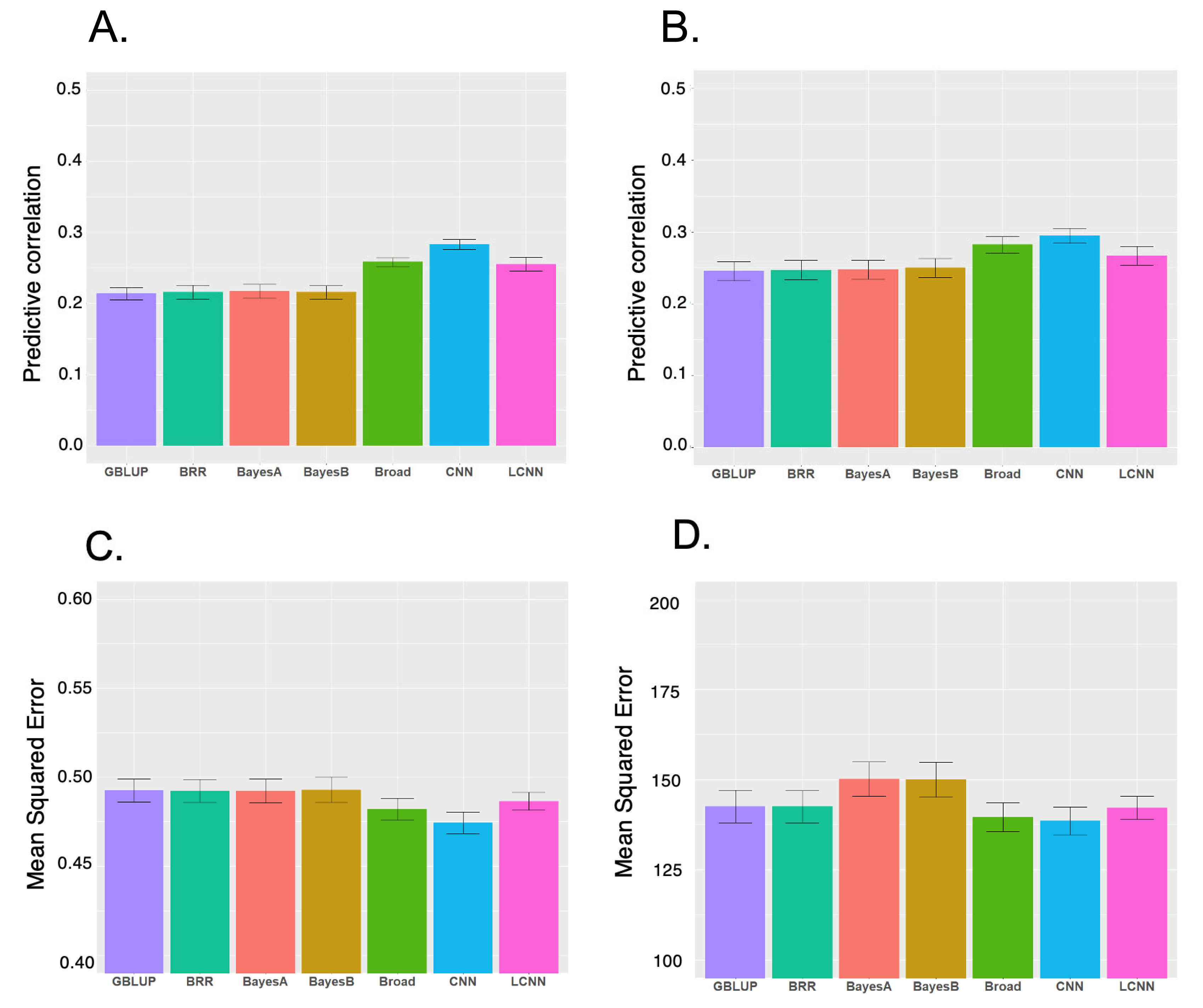
Table 1
Table 2
Table 3
| Item | Genomic prediction models | ||||||
|---|---|---|---|---|---|---|---|
|
|
|||||||
| GBLUP | BRR | BayesA | BayesB | Broad | CNN | LCNN | |
| Runtime (min) | 65 | 160 | 357 | 350 | 115 | 34 | 39 |
GBLUP, genomic best linear unbiased prediction; BRR, Bayesian ridge regression; CNN, convolutional neural networks; LCNN, local convolutional neural networks.
1) CPU, Intel Core i5-8500 CPU@3.00 GHz; GPU, NVIDIA RTX 3080.
REFERENCES
- TOOLS






 PDF Links
PDF Links PubReader
PubReader ePub Link
ePub Link Full text via DOI
Full text via DOI Full text via PMC
Full text via PMC Download Citation
Download Citation Print
Print





