INTRODUCTION
Estimation of feed intake (FI) for individual animals in a group-housed pen is often required due to mortality or abnormal weight gain of animals (Lindemann and Kim, 2007). Moreover, when a response of animals is related to total intake of a specific nutrient or energy rather than the concentration of the nutrient or energy (Baker, 1986), it is crucial to knowledge the FI of individual animals in a group-housed pen. A partitioning method (PM) was previously proposed as a procedure to estimate individual FI (IFI) for pigs group-housed in a pen (Lindemann and Kim, 2007). This method partitions the IFI of animals within the pen into IFI for maintenance (IFIm) and IFI for growth (IFIg). The IFIm is calculated based on the metabolizable energy (ME) of a diet and the mean body weight (BW) of an individual animal during the feeding period using an equation suggested by NRC (1998).
The ME for maintenance (MEm) has been estimated from various coefficients and exponents for metabolic BW (Kil et al., 2013). In NRC (1998), the use of MEm values calculated based on the metabolic BW using an exponent of 0.75 and a mean estimate of 106 as the coefficient for growing-finishing pigs: MEm, kcal/d = 106 kcal×kg BW0.75. However, Noblet et al. (1999) suggested that the exponent of metabolic BW be expressed as 0.60 rather than 0.75 for growing-finishing pigs. In NRC (2012), the MEm of growing-finishing pigs is described using the exponent of 0.60 and the mean coefficient of 197: MEm, kcal/d = 197 kcal×kg BW0.60. To our knowledge, the use of the coefficient and metabolic BW exponent for calculating MEm suggested in NRC (2012) has not been tested for the estimation of IFI.
Lindemann and Kim (2007) proposed a model for IFI estimation and compared the model with 2 other methods using simulation studies. These simulation studies used data from pigs fed individually. The application of PM to group-housed pigs has not been documented. Therefore, the objective was to test the hypotheses that the use of the coefficient and metabolic BW exponent suggested by NRC (2012) for MEm to calculate IFIm improves the accuracy of the estimates of IFI for pigs and that the PM estimates IFI of pigs fed in group-housing systems with greater accuracy compared with other methods.
MATERIALS AND METHODS
Simulation study 1
In simulation study 1, twenty-four barrows and 24 gilts with initial BW of 33.9 kg (standard deviation, SD = 2.1) were used and the animals were fed individually. Pigs were allowed ad libitum access to the diet (2,945 kcal of ME/kg) and water. Body weight of individual pigs and IFI were recorded weekly. Growth data on a bi-weekly basis were used to compare the actual and estimated IFI. The final BW of the pigs was 57.7 kg (SD = 3.7).
Within pens, the growth data of each pig were pooled, calculated, and compared according to the procedures described by Lindemann and Kim (2007). Two hundred and forty-four artificial pens were created by grouping 4 or 6 pigs in a pen. Complete randomization, randomization within blocks by BW without regard to sex, randomization within blocks by BW with balanced sex, and randomization within blocks by BW and sex were used to regroup the pigs. The experimental animal allotment program of Kim and Lindemann (2007) was used for the simulation. Lastly, the IFI estimated based on the new pens were compared with the actual IFI.
Simulation study 2
Twenty gilts with initial BW of 67.1 kg (SD = 6.1) were used in simulation study 2. Pigs had ad libitum access to the diet of 3,312 kcal of ME/kg and to water. Pigs were fed in group pens of practical farms, and individual BW of pigs and IFI records were kept daily using FIRE System (Osborne Industries Inc., Osborne, KS, USA) and Acema-128 (Acemo, Pontivy, France). The growth data on a biweekly basis were used to compare the actual and estimated IFI. The final BW of the pigs was 101.8 kg (SD = 7.4).
The growth data were pooled, calculated, and analyzed as described in simulation study 1. Thirty-two artificial pens were created by grouping 4, 5, or 6 pigs in a pen. Complete randomization was used for 5, 4, or 3 pens, which yielded the aforementioned grouping, respectively. The pigs were also blocked by BW and allotted to each pen to make 2, 3, 4, or 5 replications using the animal allotment program (Kim and Lindemann, 2007). Lastly, the IFI estimated based on the new pens were compared with the actual IFI.
Partitioning method to estimate individual feed intake
The model proposed by Lindemann and Kim (2007) partitions IFI into IFIm and IFIg. Based on the ME in feed (kcal/kg), IFIm can be calculated as:
where BW is the mean BW for the period of interest; d is the number of days in the period of interest; and MEf is the ME concentration in the feed (kcal/kg). The coefficient of 197 and exponent of 0.60 for metabolic BW is also used according to NRC (2012):
Sum of IFIm for all pigs within the pen represented as the pen FI (PFI) for maintenance (PFIm) is then subtracted from total PFI (kg), and the remainder is PFI for growth (PFIg) as:
where PFIm is the sum of IFIm for all pigs in the pen, in kilograms.
Next step is to calculate the IFIg by apportioning PFIg equally to each kg of BW gain during the period of interest within the pen:
where IBWG is the individual BW gain (kg); and PBWG is the pen BW gain whose value is the sum of IBWG for all pigs in the pen (kg).
Lastly, the sum of IFIm and IFIg is IFI for the pig in the pen as:
Ratio method to estimate individual feed intake
The ratio method (RM) does not consider the IFIm of pigs, but focuses of IBWG. This method only apportions the PFI equally to each kg of IBWG:
Averaging method to estimate individual feed intake
The averaging method (AM) does not reflect the individual’s biological aspects to the FI of pigs. All pigs in a pen are believed to have the same FI during the feeding trials as:
Comparison among methods to estimate individual feed intake
To describe the accuracy of estimation, we measured the difference using percentages. The difference between the actual and estimated IFI were calculated as:
In this study, a smaller value of the difference (%) was considered to be more accurate when there was a significant difference.
Statistical analysis
Analysis of variance and mean separation tests were performed using PROC general linear model of SAS (SAS Inst. Inc., Cary, NC, USA) with PDIFF option and Tukey’s adjustment. The model included method as a fixed variable. The experimental unit was each difference between the actual and estimated IFI from a pig, and the significance level was set at p-value less than 0.05.
RESULTS
Metabolizable energy for maintenance
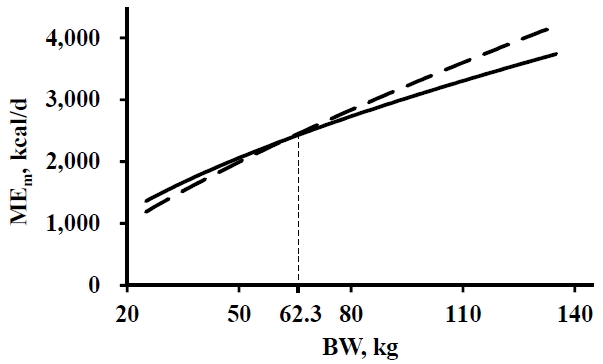
The absolute values of difference between the estimated MEm (kcal/d) based on the different coefficients and exponents for metabolic BW ranged from 0 to 459.9 kcal/d for growing-finishing pigs (Figure 1). Point of intersection where the difference in values of MEm equaled 0 was approximately 62.3 kg of BW.
Simulation study 1
In simulation study 1, the PM 1 and 2 were able to estimate IFI better than AM during any period of interest (p<0.05; Table 1). The greater accuracy of PM 1 and 2 for IFI estimation was observed than RM during d 0 to 14 and d 14 and 28, but the accuracy did not differ between PM and RM during d 0 to 28. The accuracy did not differ between AM and RM during any period of interest. Lastly, the criterion also did not differ between PM 1 and 2 during all periods.
Simulation study 2
In simulation study 2, the PM 1 and 2 were able to estimate IFI better than AM during d 0 to 14, d 14 to 28, and d 0 to 42 (p<0.05; Table 2), but the criterion did not differ between PM 1 or 2 and AM during d 28 to 42. The PM 1 and 2 estimated IFI better than the RM during all periods (p<0.05). The RM showed less accuracy (p<0.05) in estimation of IFI than AM during d 28 to 42, but the accuracy did not differ between AM and RM during d 0 to 14, d 14 to 28, and d 0 to 42. Again, the accuracy of PM 1 and 2 for IFI estimation did not differ during any period.
DISCUSSION
The PM 1 and 2 consistently showed greater accuracy in estimation of IFI than AM and RM in both simulation studies 1 and 2. Lindemann and Kim (2007) validated the PM as a model to estimate IFI that is represented by PM 2 in the present study and found greater accuracy of PM than AM and RM in individual-housing system. This result was consistent with the present study. Feed intake for maintenance is an important factor to estimate IFI because PM 1 and 2 showed greater accuracy in most of the periods in simulation studies 1 and 2 than RM which calculates IFI based on only IBWG of pigs. Additionally, the results from the simulation study 2 showed that the PM may be applied to estimate IFI with fairly good accuracy in the group-housing systems. Turner et al. (2003) reviewed the previous studies of different group size (3<pigs/pen<100) and found no correlation between the average daily FI of growing-finishing pigs and the group size.
The IFI estimated based on AM may be attained with reliable values when the actual IFI are homogenous among the pigs within a pen. In the simulation study 2, however, the variation in FI among pigs during d 28 to 42 was similar to that of other periods (coefficient of variation = 10.1%, 11.1%, and 11.4%, respectively for d 0 to 14, d 14 to 28, and d 28 to 42). The different responses among the periods may be partly explained by the different physiological states such as a digestive physiology of pigs. Digestibility of the nutrients is one of the major factors affecting the accretion of proteins and lipids (Harris et al., 2012), but Kim et al. (2007) failed to find the effects of BW on the dry matter digestibility within the weanling, growing, and finishing stages. In this study, the growing and finishing pigs were used and whether the digestibility was affected by the different stage was not clear.
On the other hand, pigs showed greater variation in gain to feed ratio during d 28 to 42 than other periods in simulation study 2 (coefficient of variation = 10.7%, 11.7%, and 17.8%, respectively for d 0 to 14, d 14 to 28, and d 28 to 42). When the gain to feed ratio showed large variation among the pigs, accurate IFI may not be attained by PM because gain to feed ratio represents performance traits of animals such as BW gain and FI and because PM calculates the IFI based on the IBWG and FI of pigs. Indeed, greater difference between estimated and actual FI was observed during d 28 to 42 than other periods (Table 2).
The accuracy of PM 1 and 2 for IFI estimation did not differ for IFI of pigs during any period tested in the simulation studies 1 and 2. The MEm estimated using the equation suggested by NRC (1998) becomes greater than MEm estimated using the equation suggested by NRC (2012) as the BW of pigs exceeds 62.3 kg (Figure 1). The mean BW of pigs for the total period of simulation studies 1 and 2 were 48.6 and 84.4 kg, respectively. The absolute difference between the respective MEm values of pigs with BW of 48.6 and 84.4 kg calculated based on the equations suggested by NRC (1998) and NRC (2012) were 74.0 and 132 kcal/d, which accounts for small portion of the daily FI when the MEm was divided by ME in the diets.
CONCLUSION
The results from this study demonstrate that the use of 197 kcal×kg BW0.60 as MEm in PM does not improve the accuracy of IFI estimates compared with the use of 106 kcal×kg BW0.75, and that partitioning the IFI into IFIm and IFIg provided the IFI of the pigs with greater accuracy compared with an AM or RM in group-housing systems.
PDF Links
PubReader
ePub Link
Full text via DOI
Full text via PMC
Download Citation
Print
