INTRODUCTION
MATERIALS AND METHODS
Data
Figure┬Ā1

Methods
LASSO (Tibshirani, 1996)
Fused LASSO (Tibshirani et al., 2005)
Elastic net (Zou and Hastie, 2005)
Comparing methods
Partition the data into the first-deep training and validation sets; then partition the first-deep training set into the second-deep training and test set (two-deep CV).
At the second-deep, construct the model using the sub-training set and calculate CV; then choose the optimal tuning parameter that minimizes CV.
At the first-deep, fit the model and estimate the coefficients in the first-deep training set with the estimated regularization parameter from the second-deep set.
RESULT AND DISCUSSION
Table┬Ā1
Table┬Ā2
| Fold | Regularized regression | ||
|---|---|---|---|
|
|
|||
| LASSO | Fused LASSO | Elastic net | |
| 1 | 0.3627 | 0.4150 | 0.3972 |
| 2 | 0.6802 | 0.6978 | 0.6966 |
| 3 | 0.6136 | 0.6410 | 0.6239 |
| 4 | 0.5600 | 0.5848 | 0.5694 |
| 5 | 0.7295 | 0.7510 | 0.7338 |
| 6 | 0.5973 | 0.6265 | 0.6011 |
| 7 | 0.4849 | 0.5126 | 0.4925 |
| 8 | 0.5931 | 0.6070 | 0.5962 |
| 9 | 0.5200 | 0.5422 | 0.5291 |
| 10 | 0.5708 | 0.5891 | 0.5777 |
| Ave corr1 | 0.5712 | 0.5967 | 0.5818 |
Table┬Ā3
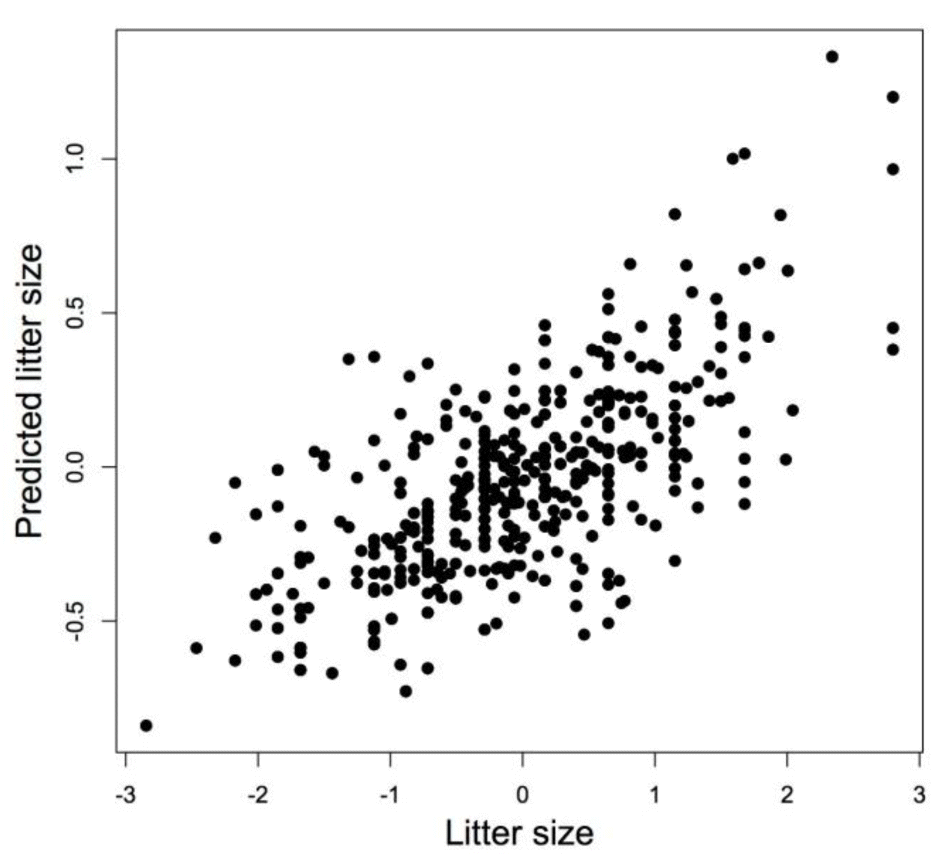
Figure┬Ā4
Table┬Ā4
| Name of SNP | Coef2 |
|---|---|
| M1GA0023299 | 0.0099 |
| MARC0015851 | 0.0094 |
| H3GA0002658 | 0.0084 |
| ASGA0001125 | 0.0074 |
| ALGA0106999 | 0.0069 |
| MARC0016306 | 0.0068 |
| ASGA0080059 | 0.0064 |
| ASGA0054467 | ŌłÆ0.0063 |
| MARC0027886 | ŌłÆ0.0064 |
| MARC0023564 | ŌłÆ0.0064 |






 PDF Links
PDF Links PubReader
PubReader ePub Link
ePub Link Full text via DOI
Full text via DOI Full text via PMC
Full text via PMC Download Citation
Download Citation Print
Print







