Linkage Disequilibrium Estimation of Chinese Beef Simmental Cattle Using High-density SNP Panels

Article information

Abstract

INTRODUCTION

Linkage disequilibrium (LD) denotes non-random association between alleles at different loci. LD is the theoretical basis of genomic selection (GS) and genome-wide association study (GWAS), that is also important in gene mapping, estimates for effective population size, population structure and so on (Nachman, 2002). Molecular markers such as single nucleotide polymorphisms (SNPs) and microsatellites were widely used to estimate the extent of LD. The level of LD is usually influenced by non-genetic factors and genetic factors containing genetic linkage, selection, the rate of recombination, the rate of mutation, genetic drift, non-random mating and population structure.

The effective population size (N_e) is defined as the number of individuals in an ideal population that would show the same amount of dispersion of allele frequencies under random genetic drift or the amount of inbreeding as in the population under consideration, and is usually less than the absolute population size (Wright, 1938). N_e is an important parameter, as it can help to explain how cattle populations evolve and expand, and by definition describe the rate of inbreeding accumulation and loss of genetic variation. Estimates for N_e can be obtained from heterozygote excess or LD. Presently, estimates for N_e based LD data are are more frequently used than heterozygote excess, and therefore complement evolutionary studies of cattle populations (Hayes et al., 2003).

Recently the discovery of large numbers of SNP through sequencing of the cattle genome has generated extensive research in quantifying LD characteristics (Farnir et al., 2000; Odani et al., 2006; McKay et al., 2007; Sargolzaei et al., 2008; Kim and Kirkpatrick, 2009; Qanbari et al., 2010). A recent report showed that high density markers were used to study the extent of LD in Angus, Charolais and Crossbred beef cattle (Lu et al., 2012). However, similar studies were not reported in Simmental cattle which are an important economic breed of beef cattle. LD indicates population characteristics and has different pattern on each chromosome. Hence, it is necessary to study the extent of LD, and then to estimate effective population size in Simmental cattle.

China’s role in international beef markets has grown significantly in the past years, and domestic production is projected to continue to increase (Longworth et al., 2001). However, China does not have special-purpose beef cattle. To increase beef production, American, Canadian and Australian Simmental cattle have been introduced into China and crossbred with native dual-purpose Simmental cattle, which are named Chinese beef Simmental cattle. In current research, high density SNPs data from Chinese beef Simmental cattle were used to analyze the pattern of LD, and to infer the effective population size up to 2000 generations ago. Meanwhile, we evaluated the effects of minor allelic frequency (MAF) and sample size on LD estimations.

MATERIALS AND METHODS

LD estimation

Several statistics parameters were proposed to measure the extent of LD. D′ (Lewontin, 1964) and r² (Hill, 1974) were widely used in practice, but their functions are different. r² was considered to be a better descriptor of LD as it is more robust and not sensitive to changing gene frequency and effective population size (Terwilliger et al., 2002; Zhao et al., 2007).

Assume two loci A and B, each locus has two alleles (denoted A₁, A₂ and B₁, B₂, respectively). P_A1, P_A2, P_B1 and P_B2 are the frequency of each of the alleles. P₁₁, P₁₂, P₂₁ and P₂₂ show the frequency of haplotypes A₁B₁, A₁B₂, A₂B₁ and A₂B₂. Thus, r² can be expressed as:

(Equation 1) r2=(P11P12−P12P21)2PA1PA2PB1PB2

PLINK (Purcell et al., 2007) includes a set of options to calculate pair-wise linkage disequilibrium between SNPs, and to present or process this information in various ways. In this study, we used the command plink -cow -bfile filename -ld-window-r2 0 -out outname. To display the decay of LD, distances of pair-wise SNPs were binned into seven types of intervals (0 to 25 kb, 25 to 50 kb, 50 to 100 kb, 100 to 500 kb, 0.5 to 1 Mb, 1 to 5 Mb and 5 to 10 Mb) along the first 10 Mb of each chromosome, and mean r² was computed for each interval. Table 2 shows information for all the SNP pair groups.

Table 2.

Statistical information for LD over various distances

Three factors, chromosomes, MAF and sample sizes, affecting LD estimation were studied based on r² data computed above.

RESULTS

SNP statistics

SNPs information for every autosomal chromosome is given in Table 1. The total autosomal chromosome length of Chinese beef Simmental cattle was 2,541.30 Mb. The longest Bos taurus autosomal chromosome is BTA1 (length = 158.14 Mb), and the shortest is BTA25 (length = 42.80 Mb). 35,079 common SNPs between two chips covered the whole genome in this study. Average adjacent SNPs spacing was 54.17±61.44 kb, and the largest spacing situated on BTA14 was 3620 kb (between ARS-BFGL-NGS-37733 and Hapmap42739-BTA-95927). The mean MAF of the genome was 0.28±0.13, and followed an almost uniform distribution, as can be seen in Figure 1.

Table 1.

Statistical information for analyzed SNP

Figure 1.

Minor allele frequency (MAF) distribution for total SNPs.

Extent of LD across the genome

The mean values of r² for each autosomal chromosome for distance bins of 0 to 25 kb, 25 to 50 kb, 50 to 100 kb, 100 to 500 kb, 0.5 to 1 Mb, 1 to 5 Mb and 5 to 10 Mb were calculated. Table 2 shows that the average r² is 0.30, 0.23, 0.16, 0.08, 0.05, 0.04 and 0.03 at different distance bins for Simmental cattle, respectively. Figure 2 shows the LD decay over varying distances of the genome. The measured LD was high for pairs of SNPs within close proximity. However, there is a strong LD in the long distance SNP pairs.

Figure 2.

LD decay for Chinese beef Simmental cattle in whole autosomal chromosome.

The extent of LD was significantly different among chromosomes. The average r² for SNPs separated by intervals 0 to 25 kb, 25 to 50 kb, 50 to 100 kb, 100 to 500 kb, 0.5 to 1 Mb, 1 to 5 Mb and 5 to 10 Mb in each autosomal chromosome are presented in Table 3. The mean value of r² for distances less than 25 kb was 0.30, but higher for BTA9 and BTA21 (0.363 and 0.364, respectively), and lower for BTA27 (0.209). The average of r² was 0.30 in SNP pairs with physical distances of <25 kb and decreased to 0.16 at distances of 50 to 100 kb, this result was similar to that previously reported (Qanbari et al., 2010; Lu et al., 2012). A similar study found the extent of LD (r² = 0.59) in approximately 50 kb on north American Holstein cattle, which was much larger than that found in our study (Sargolzaei et al., 2008).

Table 3.

Statistical information for average r² as distance between pairs of SNP up to 10Mb for the genome

MAF and LD

In this study, three different minimum allelic frequency (MAF) thresholds (0.05, 0.1 and 0.2) were used to study the effects of MAF on the extent of LD. Figure 3 shows that MAF has a significantly effect on the mean value of r², especially over short distances (0 to 25 kb). The mean values of r² increase significantly with an increasing MAF. For example, from 0 to 25 kb, the mean value of r² for MAF≥0.05 was 0.24, however, with MAF≥0.1 and 0.2, the mean value of r² increased to 0.29 and 0.34, respectively.

Figure 3.

Average r² estimates at different physical distances for three different minor allelic frequency (MAF) thresholds. Mean LD estimates are pooled over all autosomal chromosomes, and three different minimum threshold cut off levels for minimum allele frequency are shown.

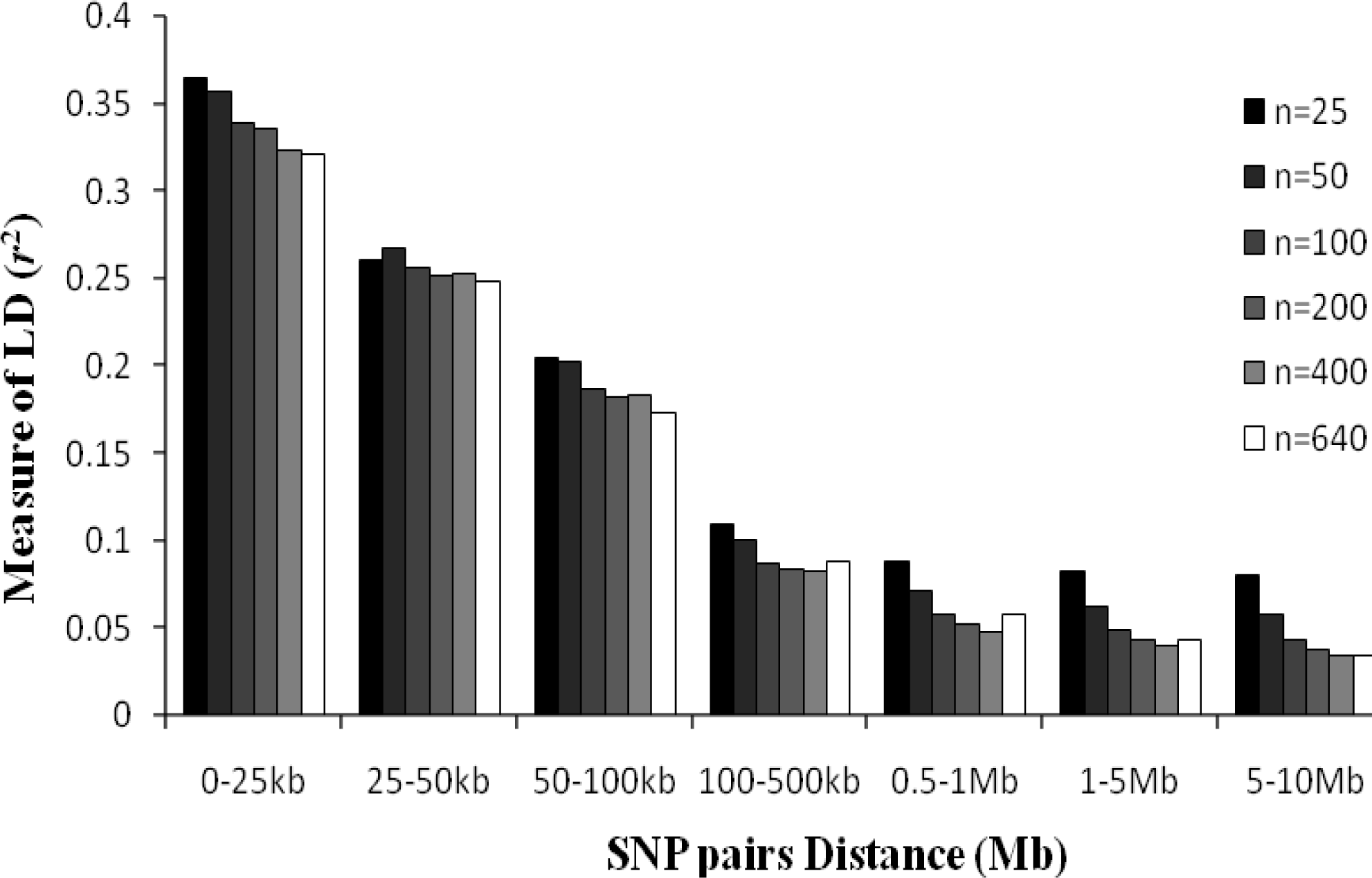
Sample size and LD estimates

As can be seen in Figure 4, sample sizes affect the LD estimation value. In this paper, five different sample sizes of n = 25, n = 50, n = 100, n = 200 and n = 400 were randomly selected from the total set to study the effect of sample size on estimates of the level of LD. The mean r² were greater when sample size is smaller, and this phenomenon is more noticeable for LD estimation across a SNP interval more than 500 kb. There were no significant differences for LD estimates when sample sizes were greater than 400 and SNP distances less than 50 kb.

Figure 4.

Average r² estimates at different physical distances for six different sample sizes. Mean LD estimates are pooled over all chromosomes, and six different sample sizes are shown.

Effective population size

The extent of LD for different chromosome fragment length could reflect the effective population size of different past generations. Table 4 shows N_e of Simmental cattle in past generations. Estimates of N_e for 2,000 generations ago was approximately 2,377 and down to 73 at 5 generations ago. Estimates of N_e for Chinese beef Simmental cattle show an increasing trend when plotted against increasing past generations (Figure 5).

Table 4.

Statistical information for effective population sizes of Simmental cattle

Figure 5.

Estimated N_e for Chinese beef Simmental cattle over time from linkage disequilibrium data.

DISCUSSION

Recent developments in high-throughput SNP panels have generated enthusiasm and interesting in GS and GWAS on cattle. Linkage disequilibrium maps can increase power and precision in association mapping. Qanbari et al. (2010) reported an average level LD of 0.30 over pair wise distances less than 25 kb based on 40,854 SNPs in 810 German Holstein cattle. Kim and Kirkpatrick (2009) reported LD of >0.80 over genomic regions of approximately 50 kb using 7119 SNPs in North America Holstein cattle. Lu et al. (2012) reported the extent of LD in Angus, Charolais and crossbred beef cattle based on Illumina BovineSNP50_v2 Beadchip and Illumina BovineSNP50_v1 Beadchip, with the level of LD being 0.29, 0.22 and 0.15 when the distance range between markers is 0 to 30 kb, respectively. This could be attributed in part to the difference in populations between the current study and previously reported research. Furthermore, in the current study, we used 35,079 SNPs distributed across the entire bovine autosomal chromosome for the analysis of LD in Chinese beef Simmental cattle. The r² statistic denotes the extent of LD. The extent of LD showed a decreasing tendency with increasing distances of the genome. The mean r² was much higher between close loci, and the result was the same as previously reported estimates (Farnir et al., 2000; Smith et al., 2006; Kim and Kirkpatrick, 2009; Qanbari et al., 2010; Lu et al., 2012). However, a low level of LD can exist between two SNPs that are closely adjacent, while markers that are more distant can show a higher than expected level of LD. This situation also appeared in linkage disequilibrium studies on human and model animals (Reich et al., 2001). It could be caused by selection, the rate of recombination, mutation and genetic drift (Nachman, 2002).

The mean r² values were different for the same fragment length on different autosomal chromosomes. Higher LD was found for BTA21. This may reflect selection for traits that are strongly influenced by QTL on this chromosome in this breed. Chinese beef Simmental cattle are a popular breed in Chinese beef production and genetic trends suggest a strong selection for growth and meat traits. A majority of studies have shown highly significant evidence for the presence of QTLs affecting meat traits (McClure et al., 2010) on BTA21. In addition, when selection operates at a locus, the neighboring loci in close linkage with the locus under selection will have an enhanced extend of LD. When selection occurs at multiple loci in epistasis, LD between loci under epistatic selection and their tightly linked loci will be created and enhanced (Du et al., 2007).

Estimates of LD across the whole genome could be affected by many factors. In this study, removing SNPs with very low MAFs also lead to lower numbers of SNPs available for study, which can also lead to bias of LD estimates. There are several published papers observing a similar phenomenon in other species (Khatkar et al., 2008; Yan et al., 2009; Qanbari et al., 2010). LD estimation is greater with MAF increasing at a short SNP pairs distance, but the phenomenon is not sensitive when SNP pairs achieve a distance of 1 Mb. Sample size is another factor that affects estimation of the extent of LD (Khatkar et al., 2008; Yan et al., 2009). A small sample size (n = 25) can also lead to the biased estimates for LD. However, there are no significant differences for the mean r² when sample sizes exceed 100, especially when the given extent interval of LD is less than 100 kb. In addition, previous research on Holstein cattle demonstrated that a sample of 400 or more was required for reliable estimation of LD (Khatkar et al., 2008). A similar study in humans that found sample sizes would be even higher, which may be due to humans having a larger effective population size (Chen et al., 2006).

Hill (1974) proposed a method for estimating effective population sizes. In this method, estimates of N_e depend on the number of animals alive at any time and the variance of progeny number per sire. In addition, previous research showed that the latter played a key role in the decrease of the population size (Mukai et al., 1989; Nomura et al., 2001). To maximize the net response in economic merit for dairy cattle, FAO (1998) reported an effective population size of 50 per generation was required to maintain the fitness in a breed. Goddard and Smith (1990) suggested a minimum effective number of 10 bull sires per generation, equivalent to 40 individuals per generation. McParland et al. (2007) used this traditional method to estimate N_e for 550,591 Ireland Simmental cattle, the result showed that N_e was 127 at the current generation. However, pedigree information was often missing or error that caused the decline of N_e estimated accuracy. In our study, the estimate for N_e of Chinese beef Simmental cattle was approximately 73 for 5 generations ago, well above the reported numbers. This could be attributed to a sufficiently large number of sires being used to produce animals in the current dataset, and thus a small variance of family size was generated. The slope of the N_e suggests that the population sizes were decreasing consistently fast, possibly due to the use of artificial selection, and therefore actions is required to maintain a larger N_e.

Article information Continued