Application of random regression models for genetic analysis of 305-d milk yield over different lactations of Iranian Holsteins
Article information
Abstract
Objective
During the last decade, genetic evaluation of dairy cows using longitudinal data (test day milk yield or 305- day milk yield) using random regression method has been officially adopted in several countries. The objectives of this study were to estimate covariance functions for genetic and permanent environmental effects and to obtain genetic parameters of 305-day milk yield over seven parities.
Methods
Data including 60,279 total 305–day milk yield of 17,309 Iranian Holstein dairy cows in 7 parities calved between 20 to 140 months between 2004 and 2011. Residual variances were modeled by homogeneous and step functions with 7 and 10 classes.
Results
The results showed that a third order polynomial for additive genetic and permanent environmental effects plus a step function with 10 classes for the residual variance was the most adequate and parsimonious model to describe the covariance structure of the data. Heritability estimates obtained by this model varied from 0.17 to 0.28. The performance of this model was better than repeatability model. Moreover, 10 classes of residual variance produce the more accurate result than 7 classes or homogeneous residual effect.
Conclusion
A quadratic Legendre polynomial for additive genetic and permanent environmental effects with 10 step function residual classes are sufficient to produce a parsimonious model that explained the change in 305-day milk yield over consecutive parities of Iranian Holstein cows.
INTRODUCTION
In many countries, 305-day milk yield is a basis for evaluating the breeding value of dairy cows. Different analyses for milk yield were proposed in literature such as repeatability model, multiple trait model and recently random regression model (RRM). Repeatability model assuming homogeneity of variance and the equal genetic correlation between lactations. Longitudinal traits can be analyzed by a multiple trait model which can allow different genetic correlation (commonly unstructured covariance) between records on the same individual. Random regression has been used in most studies to model the additive and permanent environmental effects with homogenous or heterogeneous residual effect [1]. RRM allows changes in variance along the trajectory and provides the accurate estimation of breeding value compare to repeatability and multiple trait models [2]. The Mean trend of milk yield or 305-day total yield can be modeled with different orders of orthogonal Legendre polynomial because Legendre polynomial produces the lower correlation between parameters than other functions [3]. In RRM, it is possible to analyze test day records of milk yield or total lactation yield which each test day record or total 305-day milk yield can be treated as a separate trait. Hammami et al [4] found estimates of heritability of 305-day milk yield in the first three lactations using RRM as 0.17, 0.18, and 0.18 respectively. Many studies show that in Iran, the genetic evaluation of 305-day total milk yield is carried out using the animal model. So the objectives of this study were estimation and assessment of genetic parameters and variance components of 305-day milk yield using repeatability and different RRM.
MATERIAL AND METHODS
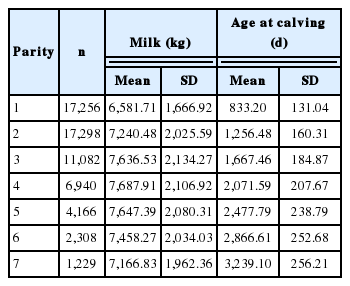
The dataset comprised a random sample of 60,279 total 305-day milk yield of 17,309 Iranian Holstein dairy cows in 7 parities from 3,776 contemporary groups (herd-year-season of calving) (HYS) that calved between 2004 and 2011. Season of calving were spring (April through June), summer (July through September), autumn (October through December) and winter (January through March). The observations were grouped into 121 classes of age at calving (AC) from 20 to 140 months of age. The pedigree file included 1,672 sires and 11,541 dams. The simple statistics of the final data file used for analysis are in Table 1.
A total of ten models including repeatability and different RRMs with various orders of Legendre Polynomials for additive and permanent environment effects and residual variance structure were fitted. Residual variance were considered homogenous (hom) or heterogeneous (het) were modeled by step function with 7 (20 to 35, 36 to 50, 51 to 70, 71 to 85, 86 to 99, 100 to 120, and 121 to 140 months of age) and 10 (20 to 32, 33 to 44, 45 to 56, 57 to 69, 70 to 81, 82 to 93, 94 to 105, 106 to 117, 118 to 129, and 130 to 140 months of age) classes in total parities. The model in matrix notation can be represented as:
Where Y is the vector of observations measured in animals; b is the vector of fixed effect (HYS); a and p are vectors of additive genetic and permanent environmental effects; X, Z, and W are incidence matrixes of fixed, additive genetics and permanent environmental effects and e is the vector of residual. The assumptions of this model are:
G and P are the (co)variance of additive genetic and perma nent environmental effects, A is the relationship matrix,
Variance components were estimated by restricted maximum likelihood method, using Wombat package [5] and the models were compared by −Log L, Schwarz Bayesian information criterion (BIC) and Akaike’s information criterion (AIC). AIC is not a test on the model in the sense of hypothesis testing; rather it is a tool for Model selection. Given a data set, several competing models could be ranked according to their AIC and BIC, with the one having the lowest AIC or BIC being the best [1,3]. In the general case the AIC and BIC are:
Where K is the number of estimated parameters in the model, L is the maximized value of the likelihood function for the estimated model, P is the number of parameters estimated, r(X) the rank of the coefficient matrix of fixed effect in the model of analysis and N is the number of data. With respect to model selection AIC and BIC including two terms: penalize index which is related to number of parameters in the model and maximum likelihood function which measures the lack of model fitting. The best model in the group compared is the one that minimizes these scores, in both cases.
In RRMs, the random genetic and permanent environmental effects were estimated by means of regression on different order Legendre polynomials. The residual variances were modeled with homogenous structure or step function with seven and ten classes.
RESULTS
The corresponding Mean, total milk yield and age at calving in each parity with standard deviations are presented in Table 1. The lowest total milk yield is related to the first lactation (6,581.71± 1,666.92 kg) and total milk increased steadily till parity 4 and the decreased till parity 7. The highest 305 d milk yield in attributed to parity 4 and 5 respectively (7,687.91±2,106.92 and 7,647.39 ±2,080.31 kg). In this Table, it is shown that variation of AC from the first to the last parity increased rapidly. A summary of various random regression analysis and repeatability models with the maximum log likelihood, AIC and BIC are shown in Table 2.
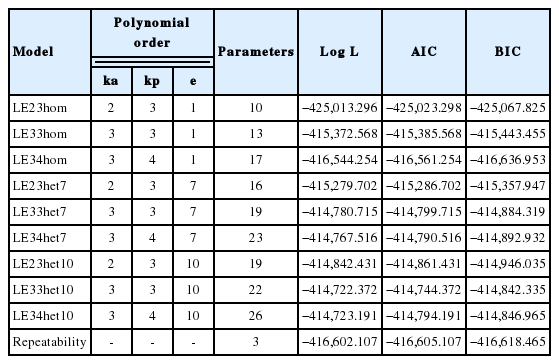
Orders of polynomials for additive genetics (Ka), permanent environment (Kp), residual variances structures (hom or het), Log L, AIC, and BIC for different random regression model
In general, the model with step functions fitted better than those with homogeneous residual and repeatability model. With increasing the number of parameters the Log likelihood (Log L) value slightly increased from −425,013.296 to −414,723.191. The average Log L for models with 10 residual classes is −414,762.664 while this value for the models with 7 residual classes is −414,942.650 respectively. Also, AIC, and BIC are smaller for models with 10 residual classes specially LE33het10 model. According to Table 2 the third order for RRM for additive genetic and permanent environmental effects with 10 residual step function class was the most adequate for fitting our data.
Phenotypic, additive genetic, permanent environmental and residual variances of the LE33het10 model during different age at calving are presented in Figure 1. Phenotypic and residual variances increased steadily from 20 months of calving and reach the highest at 137 ages at calving. These variances are lowest in the first parities and highest at the higher ages. Similar trend was observed between phenotypic and residual variance in different age at calving. The maximum and minimum phenotypic variances/1,000 at 130 and 30 months of calving were 4,844.52 and 1,127.19 while these values for residual variance were 4,067.62 and 593.07 respectively. But the trends of additive and permanent environmental variances are completely different with phenotypic and residual variances. The additive genetic variance across age at calving increased steadily till around 80 months and then drops till 130 months of calving and then tends to show a plateau till the end of age at calving. The similar trend was observed for permanent environmental effect but the highest permanent environmental variance (865.59) was shown around 80 months of calving and after that decreased till the end of age at calving. Estimates of heritability in LE33het10 and repeatability models are presented in Figure 2. Heritability estimates with LE33het10 model varied from 0.17 to 0.28 but this value for repeatability model was 0.233.

Additive genetic, permanent environmental, phenotypic and residual variances (/1,000) estimates for total milk 305-day with the best random regression model fitted (LE33het10).
Estimates of phenotypic and genetic correlations at the differ ent age at calving using LE33het10 are presented in Table 3. Both of the items showed similar pattern during various age at calving. Phenotypic correlation ranged from 0.036 to 0.528 and it was closer together between adjacent ages at calving but the range of additive genetic correlation was between 0.16 and 0.97. Lower phenotypic correlation between different ages at calving compare to additive genetic effect was obtained in this study (Table 3). According to the results, the highest genetic correlations (0.97) were observed between 78 and 108 months and 48 and 78 (0.93) months of calving. The covariance matrix of random regression coefficients for additive genetic and permanent environmental effects with the percentage of variance explained by eigenvalues associated with RRM matrix for these effects in the LE33het10 model are presented in Table 4.
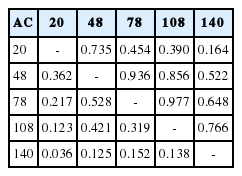
Phenotypic correlation (lower diagonal) and genetic correlation (upper diagonal) among different ages at calving in LE33het10 model
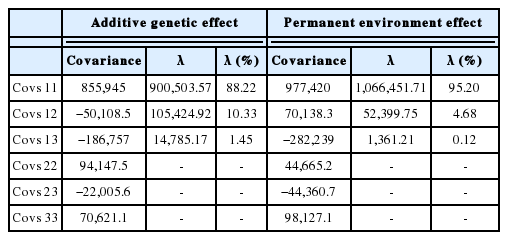
Covariance matrix of random regression coefficients for additive genetic and permanent environmental effects with eigenvalues (λ) obtained with the best model (LE33het10) in dataset
In LE33het10 model, the first three eigenvalues of additive genetics and permanent environmental covariance functions accounted 100% of total variation. The first eigenvalue of additive genetic effects was responsible for around 88% of total variance, while this value for permanent environmental effect was more than 95% and it seems that the variability of the data for additive genetic and permanent environmental effects was mainly explained by the first two eigenvalues (more than 98%).
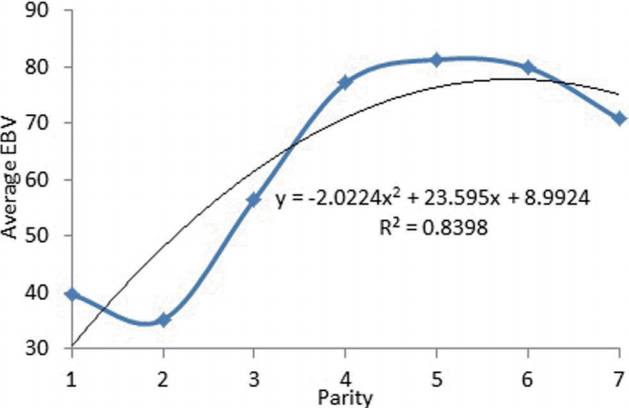
Estimation breeding value (EBV) of 305-day milk yield in different parities is shown in Figure 3. The means of breeding value for total milk yield from the first to second parity decreased from 39.6 to 35.20 but this increased gradually and reached maximum in parities 4 and 5 (81.3) and finally decreased gradually after parity 5. The change in EBV during consecutive parities showed as a polynomial function with the relatively high coefficient of determination (0.84).
DISCUSSION
Different orders of Legendre polynomial were used to describe covariance structure of longitudinal traits such as milk yields or body weight, because when both the additive genetic and permanent environmental components modeled by Legendre polynomial coefficients during time, the prediction of EBV value and variance components become more accurate [6] and the correlation between parameters are lower than compare to other functions. Results from AIC, BIC, and Log likelihood showed that homogeneous residual variance is not adequate to fit the data while models with step function, fitted the best performance. This indicates that residual variance behaves differently during within and also between different lactations. Some studies [7,8] proposed that the residual variance should be homogenous across days in milk due to limitation of program, reducing the number of parameters and dimension of the likelihood but it is better to allow residual variance to vary than to fix it in RRM because an assumption of constant error variance leads to bias in heritability estimates [9–11]. In this study, the third order of RRM for additive and permanent environmental effects is the most adequate for fitting this data set. The result is in agreement with the result of [12] which showed that the better performance of equal orders of additive and permanent environmental effects (third order) in random regression analysis of total milk yield over multiple parities in buffaloes. They also proposed a step function with 5 classes of residual variances for finding the best result. The finding indicates that with increasing of step function classes to ten and the order of fit to three for the additive genetic and permanent environmental effects, the Log likelihood increased. Our result disagrees with the finding of Guo et al [3] who reported that residual variance is constant in milking records of Danish jersey cows from the first to seventh parity. The performance of LE33het10 and LE34het10 models were similar to each other (LE33het10 is more parsimonious than LE34het10 model) but completely different and better than repeatability model (which suggested that the 305-day milk yields of different parties should not be treated as a repeated measurements of the same trait) but the genetic and permanent environmental covariances should change gradually using the optimum orders of orthogonal Legendre polynomial in random regression analysis. This means that the effects of environmental variance during different parties are considerable and one should not assume fixed during lactations in the multi-trait analysis. Most of the results reported from the multi-trait analysis are restricted to only the first three lactations. The results showed that the additive genetic and permanent environmental variance were lower at the youngest and oldest ages (around 20 and after 120 months of calving). The highest additive genetic and permanent environmental variances were observed in around 80 months of calving (fifth parity). But the patterns of phenotypic and residual variances are completely different during different parities as these components increased from the first parity to the seventh parity in LE33het10 model (Figure 1). The similar result was reported by Guo et al [3] about increasing of the phenotypic variance of total 305- day milk yield from lactation one to seven. In LE33het10 model, the residual variance estimates increased with the improvement of age at calving in consecutive parities too. It seems that the main reason of increasing of phenotypic variance after 80 months of calving is attributed to the residual part not additive and permanent environmental variances. Heritability estimates for 305-day milk yields, in seven lactations, ranged from 0.17 to 0.28 and showed the same trend as those observed for additive genetic variance estimates. But the heritability of 305-day milk yield with repeatability model was 0.23 (Figure 2). Estimates of heritability of 305-day milk yield were reported in the first three lactations in many studies. Hammami et al [4] and Muir et al [13] reported these values 0.17, 0.18, 0.18 and 0.29, 0.30, 0.32 for the first three lactations respectively. Heritability estimates with LE33het10 increased to 80 months of calving and then decreased till the end of calving ages. Our study showed that the variation in heritability mainly affected by additive genetic variance during lactation. Moreover, the heritability of 305- day milk yield is the highest in 4 to 5 years and then because of decreasing the number of records or increasing phenotypic variance, the value of heritability decreased. It expected that individual breeding values for total milk production change with parity number and reach a maximum around the fourth-fifth parity in Iranian Holstein cows. Maybe these results indicate that cows in later lactations express their genetic potential differently [4]. Yang et al [14] reported that the heritability of 305-day milk yield from 1st to 6–8th parity in Chinese Simmental cattle were 0.28, 0.30, 0.32, 0.32, 0.32, and 0.31 respectively. Estimates of genetic and phenotypic correlations between 305-d milk yield in different parities indicate that total milk yield in close parities was high compare with milk yields at parities that were further apart (Table 3). The largest generic correlations occur between yields in adjacent lactations resulting from a multiple trait random regression analysis [15]. Genetic correlations over parities were greater than corresponding phenotypic correlations as the largest genetic correlations occurred between 78 and 108 months of calving while the lowest were between 20 and 140 months of calving respectively. Despite closer genetic correlation from unity in adjacent ages, these values are different in various ages at calving, and it should necessary to consider 305-day milk yield in each parity, as different traits. Eigenvalues represent the amount of variation explained by the corresponding eigenfunction [16]. For each eigenfunction, a specific eigenvalue is associated as the first two eigenvalues for additive genetic and permanent environmental effects account for more than 98% of the total variation while the first three eigenvalues of the additive genetics and permanent covariance function accounted for at least 99.5% of the variations. Togashi et al [17] showed that the main three eigenvalues and associated eigenfunction explain the highest additive genetic variance independent of polynomial order should be utilized in the analysis of test day records of dairy cattle. The finding stated that third order of fit for genetic and permanent environmental effects was sufficient in the fitting of total 305-day milk yield in different parities using RRM. Based on eigenvalues for random effects, LE33het10 model reveals the best order of fit and more accurate in the dataset. Moreover, it seems that, the order of Legendre polynomial needs to be equal for additive genetics and permanent environmental effects to produce the equal chance for these effects during different parities. Trends of EBV showed clearly that significant progress was achieved during consecutive lactations. The fluctuation of EBV is high in the first and latter parities. Quadratic regression quantified this progress as 23.5 kg/parity during lactation one to seven. In many studies, genetic and phenotypic trends were reported based on test day milk yields or 305-day milk yield in the first lactation. These trends showed an annual increase during different calving years. Moreover, Reents et al [18] reported that the genetic trend from test- day models is higher than lactation models. But in our study, the maximum value for EBV was obtained in fourth and fifth parities. Similar trends were obtained in heritability and EBV 305-day milk yield and it indicates that the role of increasing total milk yield and additive genetic effects till the fourth and fifth parities are responsible for the improvement of breeding values but after these ages, the role of residual variance or temporary variance effects is determinative in Iranian Holstein cows.
IMPLICATIONS
The goal of this study was the estimation of variance components and genetic parameters of total 305-day milk yields over seven parities from 20 to 140 months of calving using different RRMs. The results from Log likelihood, AIC and BIC indicated that using a quadratic Legendre polynomial for additive genetic and permanent environmental effects with 10 step function residual classes are sufficient to produce a parsimonious model that explained the change in 305-day milk yield over consecutive parities. The contemporary group was herd- year season of calving. The heritability estimated with repeatability model was 0.233 while in LE33het10 model, heritability (which increased with age of calving till 80 months of calving and then decreased to 140 months of calving) ranging from 0.17 to 0.28. The highest genetic and permanent environmental variance were obtained around 80 and 85 months of calving respectively while residual and phenotypic variance increased steadily from 20 till 140 months of calving. Genetic correlations among different calving ages were generally greater than phenotypic correlations.
ACKNOWLEDGMENTS
The center of animal breeding of Iran is greatly acknowledged for supplying the data used in this study.
Notes
CONFLICT OF INTEREST
We certify that there is no conflict of interest with any financial organization regarding the material discussed in the manuscript.