Investigations on Genetic Architecture of Hairy Loci in Dairy Cattle by Using Single and Whole Genome Regression Approaches
Article information
Abstract
Development of body hair is an important physiological and cellular process that leads to better adaption in tropical environments for dairy cattle. Various studies suggested a major gene and, more recently, associated genes for hairy locus in dairy cattle. Main aim of this study was to i) employ a variant of the discordant sib pair model, in which half sibs from the same sires are randomly sampled using their affection statues, ii) use various single marker regression approaches, and iii) use whole genome regression approaches to dissect genetic architecture of the hairy gene in the cattle. Whole and single genome regression approaches detected strong genomic signals from Chromosome 23. Although there is a major gene effect on hairy phenotype sourced from chromosome 23: whole genome regression approach also suggested polygenic component related with other parts of the genome. Such a result could not be obtained by any of the single marker approaches.
INTRODUCTION
Genome wide association studies (GWAS) are employed to detect single nucleotide polymorphisms (SNP) associated with phenotypes in domestic species. Assumptions regarding underlying genetic architecture are important in association mapping for detecting genetic factors related with the phenotypes of interests (de los Campos et al., 2015). To date single regression tests based on SNPs have been commonly employed in GWAS. Discordant sib pair (DSP) model is one application of single SNP models in association mapping (Boehnke and Langefeld, 1998). DSP design uses matched sib pairs (as cases and controls) from the same families to reduce impact of environmental effects and to increase genetic homogeneity to overcome population stratification problems for association mapping. Karacaören et al. (2010) and Karacaören (2012) suggested the use of DSP design in domestic species based on availability of larger number of sib pairs in animal genetics (due to controlled crosses) compared with humans.
However only a small proportion of the genetic variance could be explained by using single SNP regression approaches in GWAS. This phenomena is termed as “missing heritability” (Turkheimer, 2011) in genomics. To overcome this problem Visscher (2008) and Yang et al. (2010) suggested using whole SNPs simultaneously similar to Meuwissen et al. (2001) approach. Meuwissen et al. (2001) proposed to use genomic selection models based on usage of whole markers simultaneously to predict total genetic value of the animals. Genomic selection (prediction) models also are suggested in GWAS to detect associated variants (de los Campos et al., 2010; Fernando and Garrick, 2013) instead of single SNPs models. Employing whole markers altogether in a GWAS might be beneficial for multiple hypothesis testing, linkage disequilibrium and for increasing the power of the study (Moser et al., 2015).
Development of body hair is an important physiological and cellular process that leads to better adaption in tropical environments for dairy cattle (Dikmen et al., 2013). Various studies suggested a major gene (Olson et al., 2003) and, more recently, associated genes (Dikmen et al., 2013; Littlejohn et al., 2014) for hairy locus in dairy cattle. Main aim of this study was to i) employ a variant of the DSP model, in which half sibs from the same sires are randomly sampled using their affection statues, ii) use various single SNPs regression approaches (Price et al., 2006; Aulchenko et al., 2007) and iii) use whole genome regression approaches (Moser et al., 2015) to dissect genetic architecture of the hairy gene in the cattle.
MATERIAL AND METHODS
Data
The pedigree included 99 Holstein-Friesians formed by 22 nuclear trios and 77 half sib offspring. Half sib offspring were founded by two sires. For DSP design we used the half sibs offspring of the sire “24230079” (n = 50). Hairiness phenotypes were assessed by visual inspection of the cattle and recorded as a binary trait. The genome consisted of 712,122 SNPs distributed over 29 chromosomes. More details about the dataset could be found at Littlejohn et al. (2014).
Genome wide association analyses
Linear mixed models could be used to test for genome wide association (Zhou and Stevens, 2012). Due to the effect of half sib family structure the genetic stratification needs to be taken into account. We used genomic pedigree information in linear mixed model to take into account of the half sib structure as was implemented in GenABEL (Aulchenko et al., 2007) using genomewide rapid association with the mixed model and regression (GRAMMAR-gamma) (Aulchenko et al., 2007; Svishcheva et al., 2012) approach in R software (R development team, 2013).
The linear mixed model used as
where y contains the observations, b is the sex effects, a is the additive genetic effect, matrices X and Z are incidence matrices, and e is a vector containing residuals.
For the random effects, it is assumed that A is the coefficient of coancestry obtained from genotype of animals; I is an identity matrix,
Discordant half sib pair analyses
Discordant sib pair design defines the sib pairs as cases and controls to detect putative association based on different allele counting schemes. We here extend this approach to include half sib pairs offspring. Discordant half sib pair analyses could be used to count of marker alleles in cases and controls allocated by their half sib structures. These counts might use all alleles or those discordant alleles in half sib progenies (Table 1).
Pearson homogeneity statistic could be estimated from 2xm table via following formula;
where nij stands for counted alleles among cases and controls, i = 1, 2 for cases and controls, respectively and j = 1…m (number of alleles). Due to correlation of test statistics within half sib offspring; permutation tests could be used to assess the signification. As was defined in (Karacaören, 2012) we randomly exchanged the case and control statues of the half sib offspring with probability of 1/2 to detect significance level of the test statistics.
A Bayesian mixture model
We used a hierarchical Bayesian mixture model (Moser et al., 2015) for predicting SNP effects (BayesR). BayesR assumed a mixture of four normal distributions for the SNP effects to be predicted;
where β is the SNP effects, p is the mixture proportions (assumed to be 0.00001, 0.0001, 0.001, 0.01),
RESULTS
We excluded 139,283 SNPs based on minor allele frequency of <5%, leaving 572,839 SNPs in the dataset. We excluded 2 individuals due to too high identity by state (IBS) (0.95>) leaving 97 individuals in the analyses. Mean IBS was estimated as 0.72 (0.03) and mean autosomal heterozygosity was estimated as 0.40 (0.01). Genomic heritability was found to be 0.84.
To detect the associated locus with the hairy gene we conducted a genome wide association analyses using genomic pedigree and genomic principal component analyses. The IBS matrix and genomic principal components used in the linear mixed model should adjust and remove the genetic stratification due to the half sib family structure.
Both the GRAMMAR (Figure 1) and the principal component analyses (Figure 3) detected strong genomic signals from chromosome 23 (Tables 2 and 3). After corrections for multiple hypothesis testing by 1,000 permutations; 223 SNPs (p<0.05) and 440 SNPs (p<0.05) were declared significant with 1.19 (0.00007) and 3.31 (0.07) inflation factors by GRAMMAR and principal components approaches respectively.
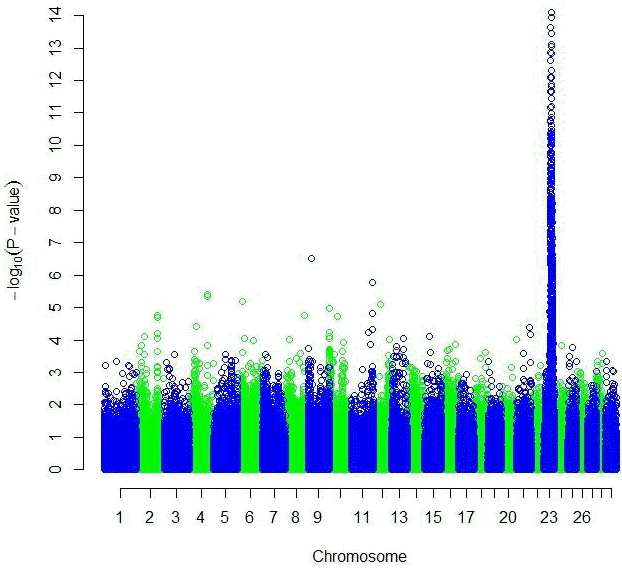
Manhattan plot of genome wide association studies result using GRAMMAR approach. The x-axis of the Manhattan plot shows the genomic position, the y-axis represents the log10 base transformed p-values.
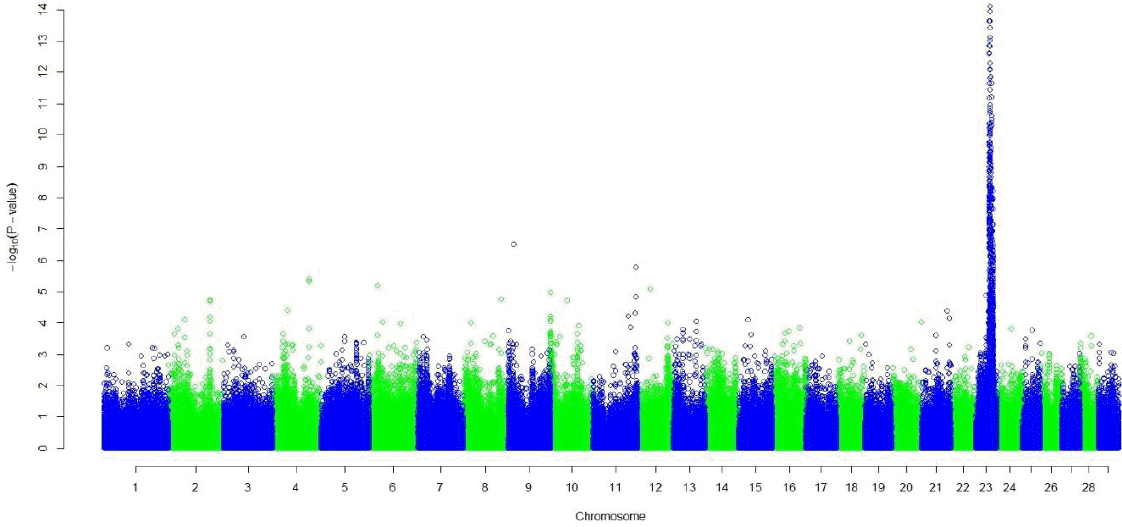
Manhattan plot of genome wide association studies result using principal components approach. The x-axis of the Manhattan plot shows the genomic position, the y-axis represents the log10 base transformed p-values.
Genotype and allele counts for a significant SNP (rs109386507) obtained by the principal component regression approach (Table 3) are presented in Table 4 and 5. Pearson homogeneity statistic was found to be 15.43 and 18.00 using allele counting Schemes 1 and 2 (Table 5). Since Scheme 2 counts only discordant alleles it is expected that test statistics and hence, evidence for the association is stronger. Due to dependency between half sib pair offspring, traditional statistical tests cannot be used in conjunction with hypothesis testing. Instead we used Monte Carlo simulations based on 100,000 permutations of hairiness phenotypes to declare significance. We detected 437 and 94 cases within 100,000 permutations for Schemes 1 and 2 respectively. Hence level of significance were found to be 0.004 and 0.0009 using Schemes 1 and 2 respectively.
We assumed that SNPs effects were taken from the normal distribution with different mixture proportions. Such an assumption is possible since SNPs might have different proportions of explanatory variances on the phenotypes. We ran the Markov chain algorithm 4 times and investigated the trace plot of number of significant SNPs. Visual inspection of the trace plots show convergence (results not shown) of Markov chains. The posterior mean number of SNPs were 23. Table 6 shows that most of the SNPs had small effects (<0.001). Largest effects were detected from Chromosome 23 (for example rs109407108 and rs137784196). Additive genetic variation explained by chromosome 23 was found to be 87%. Over all 23 SNPs explained 99% of the total genetic variance.
DISCUSSION
Both linear mixed model with genomic relationship matrix and principal components, half sib DSP analyses and a bayesian mixture model identified strong genomic signals from chromosome 23 for hairy gene. Littlejohn et al. (2014) also detected a strong genomic signal by sib transmission disequilibrium test and suggested a prolactin (PRL) as a candidate gene on chromosome 23 for hairy locus.
Both GRAMMAR (Figure 1) and principal components (Figure 3) approaches employed in this study detected similar genomic regions for hairy phenotype. However principal components approaches estimated higher inflation factors (3.31) (Figure 4) and a higher number of SNPs (440) compared with a GRAMMAR approach (1.19) (Figure 2) with lower number of SNPs (223). Since GRAMMAR gamma approach (Svishcheva et al., 2012) explicitly use gamma factors to reduce inflation factors this result is not surprising. However the larger estimates of the inflation factors do not have to reflect the population stratification (Yang et al., 2011) under especially polygenic inheritance as was also pointed out by Lee et al. (2014).
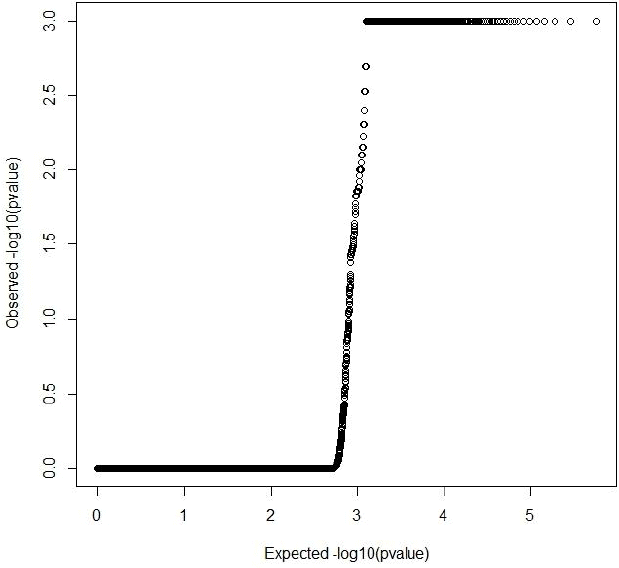
Quantile-Quantile plot of principal components genome wide association studies result. Inflation factor (lambda) = 3.31 (0.07).

Quantile-Quantile plot of GRAMMAR genome wide association studies result. Inflation factor (lambda) = 1.19 (0.00007).
We used half sib progenies in DSP experimental design to confirm the most significant SNPs. Both counting schemes for rs109386507 (Table 4) confirmed the significance of the SNP. Increasing the number of discordant half sib progenies probably will also increase the accuracy. Since half sib family design is common in animal genetics such an extension of DSP design might be useful. Although here we used a single locus allele counting schemes for discordant half sib pair analyses it is possible to extend the model for the genome as was suggested by Boenke and Langefeld (1998). However heavy computation cost of permutations over the genome might be one limitation of the discordant half sib pair model.
Whole and single genome regression approaches detected strong genomic signals from Chromosome 23. But with a Bayesian mixture model we assumed a different degree of explanatory variances for the SNPs. In that regard, different from results of Littlejohn et al. (2014) we also detected genomic signals from chromosomes 9 (rs43610968) and 24 (rs137446885) for example. Although chromosome 23 was relatively short compared with the most of the other chromosomes; it explains 87% of total genetic variance detected by the Bayesian mixture model. More than 99% of the SNPs had tiny (or zero) effects on the genetic variance. Although there is a major gene effect on hairy phenotype sourced from chromosome 23; whole genome regression approach also suggested a polygenic component related with other parts of the genome. Such a result could not be obtained by any of the single marker approaches.
Notes
CONFLICT OF INTEREST
We certify that there is no conflict of interest with any financial organization regarding the material discussed in the manuscript.





