Phenotypic Characterization and Multivariate Analysis to Explain Body Conformation in Lesser Known Buffalo (Bubalus bubalis) from North India
Article information
Abstract
Phenotypic characterization and body biometric in 13 traits (height at withers, body length, chest girth, paunch girth, ear length, tail length, length of tail up to switch, face length, face width, horn length, circumference of horn at base, distances between pin bone and hip bone) were recorded in 233 adult Gojri buffaloes from Punjab and Himachal Pradesh states of India. Traits were analysed by using varimax rotated principal component analysis (PCA) with Kaiser Normalization to explain body conformation. PCA revealed four components which explained about 70.9% of the total variation. First component described the general body conformation and explained 31.5% of total variation. It was represented by significant positive high loading of height at wither, body length, heart girth, face length and face width. The communality ranged from 0.83 (hip bone distance) to 0.45 (horn length) and unique factors ranged from 0.16 to 0.55 for all these 13 different biometric traits. Present study suggests that first principal component can be used in the evaluation and comparison of body conformation in buffaloes and thus provides an opportunity to distinguish between early and late maturing to adult, based on a small group of biometric traits to explain body conformation in adult buffaloes.
INTRODUCTION
Phenotypic characterization is used to identify and document diversity within and between distinct breeds, based on their observable attributes (FAO, 2012). Phenotypic characterization, including information of body biometry, is the prerequisite of all lesser known buffalo populations in order to provide overall picture of buffalo genetic diversity. Unless we know the physical and biometric characters besides accurate geographic location, population size, animal husbandry management practices, and utility of the particular animal breed their overall improvement cannot be properly implemented. In India, the buffalo population is 105.34 million (56.6% of total world buffalo population) which contributes 51.1% of total milk produced in the country. About 56.0% were classified as nondescript/uncharacterized buffaloes (DAHDF, 2007). This estimate of non-descript buffaloes includes many unique but distinct buffalo populations, which needs to studied and classified. Till date, 13 breeds of buffalo have been recognized, studied and registered in India (NBAGR, 2013). One unique lesser known buffalo population which have not been studied so far is Gojri buffalo from Punjab and Himachal Pradesh (Vohra et al., 2012). “Gojri” means “Gujjars’ animal” and is recognised due to the community who rear them, since time immemorial. Gojri buffaloes are well adapted in hot and humid climate of India and have a unique ability to graze on hill tops without fall, a characteristic not common to riverine buffaloes. Physical appearance of Gojri buffaloes include black coat colour with brown thick hairs; white patches may be present on black face, and muzzle is black in colour. Males are brownish to black in colour. Horns are characteristic medium to large sized with curved orientation which moves backwards and then towards front to complete the loop, called ‘Pattih wale seengh’. Udder is small round shaped but well-placed with cylindrical teats and milk vein is visible indicating the potential for milk production. The temperament of these animals is docile (Figure 1).
Adult female Gojri buffalo with typical phenotype and Characteristic horn orientation.
Body conformation by recording a minimum number of body measurements/biometric traits which reduce the cost, labour and time is the need of the day. FAO have used height at withers (HT) as a prime indicator for their type (Simon and Buchenauer, 1993). Body shapes measured objectively could improve selection for growth by enabling the breeder to recognize early-maturing and late-maturing animals of different size (Brown et al., 1973; 1974). Significant differences in different body measurement/biometric traits due to age and sex were reported by many workers in different breeds and species. i.e. Gilbert et al. (1993), Shahin et al. (1995), Pundir et al. (2007a, b, c; 2008), Singh et al. (2008) and Yakubu et al. (2009) in cattle; Shahin et al. (1993) in Egyptian buffalo; Biedermann and Schmucker (1989), Jakubec et al. (1999), Miserani et al. (2002) and Sadak et al. (2006) in horses; and Sarako et al. (2006) in sheep. In the present study different body biometry traits, relationships among different body measurements and to develop unobservable components (latent) to define which of these measures best represent body conformation in Gojri buffalo were studied using principal component analysis.
MATERIALS AND METHODS
Data consisted of 13 different body measurements which can explain the body conformation in buffaloes were taken on a lesser known buffalo sample, popularly known as Gojri, from Punjab and Himachal Pradesh regions of North India. Traits included in the study were height at wither or body height (HT); body length (BL); chest girth (CG); paunch girth (PG); face length (FL); face width (FW); horn length (HL); horn circumference (HC); ear length (EL); distance between hip bone (HB); distance between pin bone (PB); tail length (TL); tail length up to switch (TUS). To avoid age and sex effects only adult Gojri buffaloes (3.5 yrs and above) were taken in the study. Biometric data on 233 Gojri buffaloes was collected from four districts of their breeding tract. All the measurements were recorded once in upright animal standing on a level ground and by the same technical person to avoid between-recorder effects. Measurements were recorded by using tape measure.
Statistical analysis
To study the effect of district on all recorded body measurements, data were analyzed using first model of Harvey (Harvey, 1987).
Where, Yij is the observation of one of the 13 biometric traits, μ is the overall mean, Di and is the fixed effects of district while eij is the random residual error associated with each observation which is normally and independently distributed with mean zero and unit variance. Data for all the biometric traits were subject to least square analysis with district as fixed effect and there was no significant effect (results not shown) on any of these traits.
Physical characterization of adult buffaloes and phenotypic correlations between different body biometric traits were estimated using partial correlations. All the analysis was carried out using the SPSS (2001) statistical package for social sciences. When the recorded traits are correlated then principal component analyses (PCA), a multivariate approach, which reduces the dimensionality of a data set, is used. The PCA can explain relationships between different body biometry traits in a better way.
Principal component analyses and rotation of factors
The PCA is a multivariate statistical techniques dealing with the reduction of a set of observable variables. The objective of PCA is to account for the maximum portion of the variance present in the original set of variables with a minimum number of composite variables. Varimax rotation was used for rotation of principal components through the transformation of the components to approximate a simple structure. Kaiser-Meyer-Olkin (KMO) test of sampling adequacy and Bartlett’s test of sphericity were computed to establish the validity of data set, at 1% level of significance. There are two techniques that can be used for data reduction (factor analysis and PCA) and both are functionally the same and used for the same purpose. However, they are quite different in terms of underlying assumptions. Factor analysis assumes that a variable’s variance can be decomposed into two parts (Johnson and Wichern, 1982). The first part is called common variance (communality factor) that is shared by other variables included in the model. The estimate of communality for each variable measures the proportion of variance of that variable explained by all the other components jointly. The second part is called specific variance (unique factor) as it is specific to a particular variable and includes the error variance. Factor analysis deals only with the common variance of the observed variables. However, principal component analysis considers both the total variance and unique variance and does not make any differentiation between these two. The objective of factor analysis is the reduction of the original variables into a limited number of unobservable latent factors (variables) that are extracted to account for inter-correlation among the observed variables and to explain why these variables are correlated with each other. It assumes that the unique variance represents a significant portion of the total variance. On the other hand, the objective of principal component analysis is to account for the maximum portion of the variance present in the original set of variables with a minimum number of composite variables. It assumes that the unique variance represents a small portion of the total variance (Sadak et al., 2006). In the present study Varimax rotation was used for rotation of principal components through the transformation of the components to approximate a simple structure.
RESULTS AND DISCUSSION
Mean of biometric traits (cm) studied in Gojri buffaloes were 128.66±0.32 for HT, 133.33±0.35 BL, 195.91±0.67 CG, 213.91±1.34 PG, 48.58±0.11 FL, 22.33±0.09 FW, 44.61±0.61 HL, 19.82±0.12 HC, 28.76±0.09 EL, 53.58 ±0.24 HB, 24.29±0.29 PB, 90.57±1.15 TL and 104.15± 0.67 tail up to switch, respectively. In Nilli Ravi breed of river buffalo, Nivsarkar et al. (2000) reported average HT, CG, and BL as 134.2, 207.7, and 165.4 cm respectively, whereas Ahmad et al. (2013) reported HT to be 140.2±7.2 cm in Nilli Ravi females. Based on comparison of biometric traits like average HT, CG and BL of Gojri buffaloes with Nilli Ravi buffaloes, which are also sharing their breeding tract, Gojri buffalo is lighter, smaller and shorter than Nilli Ravi buffaloes. Coefficient of variation for different biometric traits in Gojri buffaloes ranged from 3.32% (FL) to 19.41% (HL). It was observed that HL and distance between PB (17.05%), had more variability which may be due to the fact that selection was not applied for these traits or that these parts respond more to the environment than others. Similarly, the TL with switch (18.01%) had more variability than without the switch (9.11%), indicating that tail switch had more variability. Face length had little variability which may be due to the fact that it is a cephalic measurement and its close association with cranial bone. Majority of body measurements showed less variability, indicating that the Gojri buffaloes are almost similar in their body size. Correlation coefficient estimated ranged between −0.41 (EL and distance between PB) to 0.77 (HT and BL) among various biometric traits. A total of 91 correlations (in all combinations) were estimated. Among these 72 were significant of which 54 were positive correlations (Table 1). Height at withers had significant higher correlations with BL (0.77), FL (0.50), and CG (0.50) while it showed lowest correlation with PG (0.10) which was non-significant. Body length had higher correlations with CG (0.55) and FL (0.49), while BL had the lowest phenotypic correlation with TL. The FL had positive correlation with FW (0.62) and HC (0.55). The correlation between FW and HC (0.52), distance between HB and EL (0.67), TL and tail up to switch (0.51) were also high. The PG had small negative correlations with FL (−0.24), HC (−0.18), FW (−0.07), and TL (−0.05). Tail length showed negative correlation with PG (−0.58), HL (−0.05) and distance between PB (−0.31). The positive and significant (p<0.05/0.01) correlations among different biometric traits suggest high predictability among the different traits.
Phenotypic Correlation among 13 different body biometry traits in 233 adult female Gojri buffaloes
The PCA was applied to 13 body conformation traits in Gojri buffalo and KMO measure of sampling adequacy (MSA) was obtained as 0.74. The widely used and accepted method of rotation (varimax) was applied (Fernandez, 2002) as it maximizes the sum of the variances of the squared loadings (squared correlations between variables and components). The estimate of sampling adequacy KMO revealed the proportion of the variance in different biometric traits caused by the underlying components (Kaiser, 1958). The overall significance of the correlation matrix was tested with Bertlett’s test of sphericity for the biometric traits (chi-square was 1.149E3, p<0.01) was significant, it means correlation matrix is not an identity matrix and provided enough support for the validity of the factor analysis of data. The MSA below 0.5 was not accepted, and KMO-MSA greater than 0.5 is must for satisfactory factor analysis to proceed. Pundir et al. (2011) reported higher estimates of sampling adequacy as 0.891 in Kankrej cows and also Yakuba et al. (2009) as their estimates of sampling adequacy were 0.90 and 0.92 in age groups of 1.5 to 2.4 years and 2.5 to 3.6 years, respectively, in White Fulani cattle.
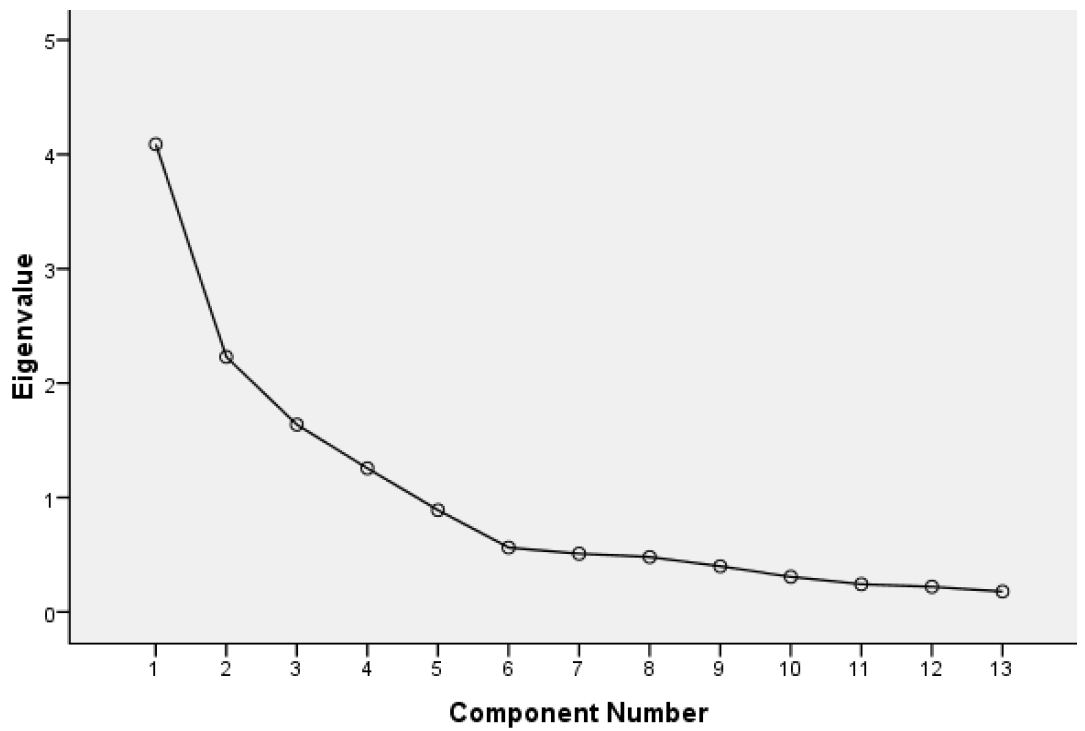
Out of 13 principal components, four components were extracted using Kaiser Rule criterion (Johnson and Wichern, 1982) to determine the number of components i.e. retaining only the components that have eigenvalue greater than 1 (Table 2). There could be more than one criterion to decide how many components can be used. Scree plot can also depict the various components and could can be used to decide the actual number of the components to be included for analysis, components having eigenvalues up to the point “bent of elbow” are usually considered (Figure 2). The identified four components could explain cumulative percentage of variance of 70.86%. First component accounted for 31.45% of the variation. It was represented by significant positive high loading of height at wither, BL, FL, FW, HL, and CG. First component seemed to be explaining the maximum of general body conformation in Gojri buffaloes. The second component explained 17.15% of total variance with high loading of distance between HB, TL, and EL. Third component explained 12.59% of variance and showed high component loadings for PG and TL up to switch. The fourth factor accounted for 9.66% of total variability with comparatively higher loading for tail characteristics (Table 3). In Egyptian buffalo bull Shahin et al. (1993) reported that most of the common variability (88%) in body dimensions could be accounted for by components representing general size, body depth and height and head width. Tolenkhomba et al. (2013) used factor analysis with promax rotation revealed 6 components which explained about 69.77% almost similar to our finding but the total variation with first component explained 21.93% of total variation and was represented by significant positive high loading of height at wither, BL, heart girth, PG, and EL in local cattle of Manipur. The proportion of total variance explained by first component was more in our study (31.45%) compared to by Tolenkhomba et al. (2013). Yakubu et al. (2009) extracted 2 factors in the age group of 2.5 to 3.6 years explained 86.47% of the total variation by studying the 14 morpho-structural traits of White Fulani cattle. Salako (2006) extracted two factors from 10 different biometric traits in Uda sheep which accounted for 75% of total variation. Sadek et al. (2006) extracted three factors for Arabian mares and stallions separately by studying 14 different traits and these explained 66% and 67% of total variation.
Total variance explained by different components in adult female Gojri buffalo (n = 233)
Scree plot showing component number with eigenvalues.
Varimax rotated component matrix of different factors for biometric traits in adult female Gojri buffalo
The communality ranged from 0.44 (HL) to 0.83 (HB distance) and unique factors ranged from 0.55 to 0.16 for all these 13 different biometric traits (Table 4). Body conformation appeared to be controlled by common and unique factors in Egyptian buffalo bulls Shahin et al. (1993). In Egyptian buffalo the communalities ranged from 0.96 (height at hips, HT) to 0.78 (rump width) and the uniqueness (special size factors) made the balance Shahin et al. (1993). Approximate range of communality i.e. 0.42 to 0.87 was reported by Sadek et al. (2006) in Arabian mares. Higher estimates of communality (ranged from 0.79 to 0.93) were observed by Yakubu et al. (2009). The lower estimates of communalities of HL and PG indicates that they did not explain the body conformation in Gojri buffaloes.
Communalities and unique factor of various biometry traits in adult female Gojri buffalo
All inter-factor correlations between different components were positive and ranged from 0.42 to 0.03, having maximum between first and second component and minimum between second and third component. Pattern Matrix indicate that the first principal component can be used in the evaluation and comparison of body biometry in female buffaloes using head and horn traits (HC, FW, and FL) while second principal component has shown high component loadings of heart girth, paunch girth, body length and height at wither (Table 5). Our findings were similar to Pundir et al. (2011) where they reported that first factor explained 38.89% of total variation and second factor accounted for 12.36% of total variability which had comparatively higher loading for horn characteristics in Kankrej cows. However, scanty literature is available for adult riverine buffaloes on body conformation traits.
Pattern matrix with varimax rotation of different factors for biometric traits in adult female Gojri buffalo
CONCLUSION
Phenotypic characterization and multivariate analysis of body conformation traits in Gojri buffalo is a novel report. The positive and significant correlations among different biometric traits suggest high predictability among the different traits, and also making them amenable for analysis through PCA. Results of PCA suggest that the use of orthogonal synthetic variables principal component one (PC1) and two (PC2) provided a means of reduction in the number of biometric traits to be recorded in Gojri buffaloes which could be used in explaining body conformation and in distinguishing different breeds. The PC1 may be used in phenotypic selection as a means to explain body conformation of better early maturing buffaloes to be used in breeding programmes.
ACKNOWLEDGMENTS
Authors wish to thank Director, NBAGR to provide financial and logistic support to carry out the work and sincere gratitude to all the livestock keepers who allowed measurements of their buffaloes. Special thanks to Mr. Subhash Chander, T-4, NBAGR for taking meticulous biometric measurements of animals under study.