 |
 |
| Anim Biosci > Volume 32(7); 2019 > Article |
|
Abstract
Objective
The objectives of this study were to compare identified informative regions through two genome-wide association study (GWAS) approaches and determine the accuracy and bias of the direct genomic value (DGV) for milk production traits in Korean Holstein cattle, using two genomic prediction approaches: single-step genomic best linear unbiased prediction (ss-GBLUP) and Bayesian Bayes-B.
Methods
Records on production traits such as adjusted 305-day milk (MY305), fat (FY305), and protein (PY305) yields were collected from 265,271 first parity cows. After quality control, 50,765 single-nucleotide polymorphic genotypes were available for analysis. In GWAS for ss-GBLUP (ssGWAS) and Bayes-B (BayesGWAS), the proportion of genetic variance for each 1-Mb genomic window was calculated and used to identify informative genomic regions. Accuracy of the DGV was estimated by a five-fold cross-validation with random clustering. As a measure of accuracy for DGV, we also assessed the correlation between DGV and deregressed-estimated breeding value (DEBV). The bias of DGV for each method was obtained by determining regression coefficients.
Results
A total of nine and five significant windows (1 Mb) were identified for MY305 using ssGWAS and BayesGWAS, respectively. Using ssGWAS and BayesGWAS, we also detected multiple significant regions for FY305 (12 and 7) and PY305 (14 and 2), respectively. Both single-step DGV and Bayes DGV also showed somewhat moderate accuracy ranges for MY305 (0.32 to 0.34), FY305 (0.37 to 0.39), and PY305 (0.35 to 0.36) traits, respectively. The mean biases of DGVs determined using the single-step and Bayesian methods were 1.50±0.21 and 1.18±0.26 for MY305, 1.75±0.33 and 1.14±0.20 for FY305, and 1.59±0.20 and 1.14±0.15 for PY305, respectively.
High production ability has been used for primary selection in dairy breeding schemes. In particular, milk yield, fat yield, and protein yield are the most important economic traits for dairy cattle selection. To date, genetic improvement of these economic traits has been performed successfully based on traditional best linear unbiased prediction (BLUP), and the breeding values of economic traits have been applied with selection indices in Korean dairy breeding systems. The BLUP used in combination with individual records and estimated breeding value (EBV) has resulted in considerable genetic progress in the dairy industry [1]. In recent years, however, genomic information in the form of commercial single-nucleotide polymorphic (SNP) marker panels from various companies (i.e., Illumina, San Diego, CA, USA; Neogen-GeneSeek, Lincoln, NE, USA; and Affymetrix, Santa Clara, CA, USA) have become available for genetic evaluations, as a consequence of improvements in genotyping technology and statistical methods after introduction by Meuwissen et al [2] in 2001. Accordingly, genomic prediction using genotypic data has been widely applied for various livestock.
Genomic selection (GS) involves selection of bulls based on genomic breeding values, which are derived from the combination of EBVs and direct breeding values (DGVs) based on SNPs using several blending formulae [3,4] or single-step methods (e.g., single-step genomic best linear unbiased prediction [ss-GBLUP]) [5] and single-step super hybrid model [6]). The advantages of GS are simplicity and resistance to preselection bias [7,8] and more reliable prediction than traditional BLUP [1,9,10]. When GS schemes are applied in the field, the use of young bulls should be the most effective in terms of reliability. For example, in young Holstein bulls in the United States, reliabilities for predicted transmitting abilities for milk yield based on genomic information ranged from 73% to 79% [11].
Typically, there are two approaches to performing GS. The first method is multiple-step GS. In step 1 of this method, pseudo-phenotypes (i.e., EBV or deregressed-EBVs), which include information related to genotyped and ungenotyped animals, are calculated for the genotyped animals; in step 2, DGV is calculated using the pseudo-records and genotyped data (i.e., Bayesian and GBLUP approaches); and in step 3, the traditional EBV and DGV are combined into genomic-enhanced EBVs (GE-EBVs). The second method is ss-GBLUP. To construct a blended relationship matrix (H-matrix) [5] using ss-GBLUP, a numeric relationship matrix (NRM) is replaced with a genomic relationship matrix (GRM) and then these can be blended with an NRM [10]. In ss-GBLUP, the accuracy obtained for milk yield is greater than that obtained using multiple-step GS [10]. However, a drawback of ss-GBLUP is that it cannot be applied to non-linear estimates, although some solutions to ss-GBLUP non-linear estimations have been presented in the literature [10].
The objectives of this study were to compare identified informative regions through two different genome-wide association study (GWAS) approaches and assess the accuracy and bias of DGVs for milk production in Korean dairy cattle using genomic prediction approaches (i.e., ss-GBLUP and Bayesian).
Raw data for the period from 1998 to 2018 were obtained from data collected by the National Agricultural Cooperative Federation’s dairy cattle improvement center by way of its milk testing program, which is nationally based. The pedigree data for this analysis were obtained from the Korean Animal Improvement Association. Traits considered in this study were adjusted 305-day (d) milk yield (MY305), adjusted 305-d fat yield (FY305), and adjusted 305-d protein yield (PY305). The data set included records for Holstein cows in the first parity with full pedigree information and excluded records with extreme milk production (MY305, <2,500 or >16,000 kg; FY305, <70 or >600 kg; and PY305, <80 or >500 kg), age at calving (<17 or >31 months). The final number of edited records was 265,271. Table 1 shows the basic statistics of the data.
Genotypic data were obtained using two SNP panels: BovineSNP50 v2 and BovineSNP50 v3 (Illumina Inc., USA). These two SNP panels were imputed to BovineSNP50 version 3 using Fimpute version 2.2 [12]. After excluding unmapped SNPs and SNPs on sex chromosomes, the available number of SNP markers was 54,931. After performing marker quality control, genotypes at each locus were excluded based on the following criteria: average call rate lower than 0.90; minor allele frequency less than 0.01; markers not in Hardy–Weinberg equilibrium, with a chi-square value (χ2) greater than 95%; and SNPs in extreme linkage disequilibrium (LD, r2 >0.99). After editing, 50,765 SNP genotypes were available for analysis. Furthermore, genotyped animals were excluded from analysis based on the following criteria: duplicate animals, twin animals, and animals that failed parentage tests. Duplicate animals and twin animals were removed based on marker call rates. Furthermore, genotype identification that could not be matched to the corresponding animal in the phenotypic data set was removed from a total of 2,032 Holstein dairy cattle. Finally, for ss-GBLUP for all traits, the genotype data set comprised 1,919 animals, whereas for Bayes-B, the number of animals available for MY305, FY305, and PY305 was 963, 943, and 946, respectively.
Genetic components, breeding values, and corresponding reliabilities of milk production traits were estimated using following mixed-model equation:
where yijk is the observation; HYSi is the fixed effect of the ith herd-year season; agej is the fixed effect of the jth calving age; ak is the random genetic effect of animal k; and eijk is the residual effect. Using a univariate animal model, the covariance between traits was assumed to be zero. In matrix notation, the statistical model with single traits was as follows:
where y is the matrix of observations for the traits; X and Z are the known incidence matrices for fixed and random effects; b is the vector of fixed effects; a is the vector of additive genetic effects for each animal, and e is the vector of the residual effect.
Total phenotypic variance (
σ p 2 σ a 2 σ e 2 h 2 = σ a 2 σ p 2
The reliability of breeding value was then calculated as:
1 - P E V / σ a 2
The ss-GBLUP was used to predict DGVs (DGVss) and analyze genome-wide association study data (ssGWAS). The ss-GBLUP method is a modification of BLUP. The numerator relationship matrix (A−1) was replaced by an H−1 matrix (a combination of numerator relationship matrix and GRM) as follows:
where A22 is a numerator relationship matrix for genotyped animals and G is a GRM. The genomic matrix (G) is formed based on [3] as follows:
where Z is the incidence matrix for markers, D is a weight matrix for SNPs (initially D = I), and q is a weighting factor. The weighting factor can be obtained by using either SNP frequency [3] or by guaranteeing that the average diagonal in G approaches that of A22 [8]. In the present study, for increasing the weights of SNPs with large effects and decreasing those with small effects, the SNP effect and weighting factor were derived using several steps, which are described by Wang et al [14]. In the present study, the weighting factor used second iteration and all procedures were performed using the BLUPF90 family [13].
Deregressed-estimated breeding value (DEBV) adjusting for parental average (DEBV-PA) values, which contained only phenotypic information for individuals and their descendants used for deregression (dividing by the reliability of EBV) with parental information [9], were used as response variables for prediction of DGVBayes and GWAS (BayesGWAS) in the multiple-step process. To ensure the quality of DEBV-PA values, those animals with a reliability of less than 0.10 were removed. To account for the heterogeneous variance of DEBV, the response variable was weighted because each animal has different reliabilities. The weighting factor (wi) [15] for animal i was calculated as follows:
where
r i 2
To estimate SNP marker effects, the Bayes-B method was used [2] with π set to 0.99. The Bayes-B method assumes that some proportion (π) of SNP markers has zero effects and that each SNP marker has locus-specific variance, which contrasts with the Bayes-C method. For each trait, marker effects were estimated using the following model equation:
where yi is DEBV on animal i for the respective trait; μ is the population mean; k is the number of markers; Zij is the allelic state at locus j in individual i; uj is the random substitution effect for marker j, which follows a mixed distribution for this random substitution effect according to indicator variable (δj), a random 0/1 variable indicating the absence or presence of marker j in the model, with uj assumed to be normally distributed
N ( 0 , σ u 2 ) N ( 0 , σ e 2 )
The posterior distributions of the parameters and effects were obtained using Gibbs sampling. We performed a Markov chain Monte Carlo (MCMC) simulation of 110,000 rounds with Gibbs sampling, of which the first 10,000 iterations were discarded as burn-in. To estimate posterior means and variances of marker effects, Metropolis–Hastings samples were run for 10 iterations. The prior genotypic and residual variances from the results of REML were used, which were implemented in the BLUPf90 family. All procedures were implemented using GenSel4R software [17].
Detection of informative regions or loci based on single SNPs may result in noise or underestimation due to the high ratio between the number of SNPs and the number of genotyped animals [14], and adjacent SNPs may be in high LD with the same quantitative trait locus (QTL) in high-density SNP panels because the effect of the QTL would be spread over all SNPs in high LD [18]. For this reason, non-overlapping 1-Mb windows, which is the proportion of genetic variance in each region consisting of a 1-Mb genome window, were calculated and used to identify informative genomic regions accounting for LD, which is more appropriate than using single SNPs.
The significance level of the informative 1-Mb window re gion in ssGWAS and BayesGWAS was, respectively, 1.0% and 0.5% of additive genetic variance, which was estimated as a portion of the total genetic variance explained by all SNPs.
To estimate the accuracy of DGVs, we applied five-fold cross-validation with random clustering, whereby we set up training data sets, each of which was each constructed by masking the phenotype in the SS-method (i.e., setting the phenotype of genotyped cows and daughters of genotyped sires and their “unknown”) and the response variable in the Bayesian method (i.e., setting the response variable “unknown”), whereby 20% of the total individuals is set to random without replacement so as to be masked precisely once in the training data sets. Using these steps, we produced five training and testing sets. This results in each genotyped animal having DGVss and DGVBayes values from the masking data set, as derived using the single-step and Bayesian methods, respectively. The correlation coefficient between the DGV and DEBV values was calculated and used as a measure of the accuracy of DGV. Additionally, the bias (spread) of DGV for each method was assessed using regression coefficients. Table 2 summarizes the number of masked animals and phenotypes in each data set.
Variance components and heritability were estimated from regular phenotypic BLUP based on a univariate animal model. The estimated heritabilities for MY305, FY305, and PY305 were 0.26, 0.21, and 0.22, respectively (Table 3).
Using association analysis based on ssGWAS and BayesGWAS, we detected the most significant regions for SNP markers on the Illumina BovineSNP50 panel. Figures 1, 2 shows plots of genetic variance accounted for by 1-Mb windows, within a chromosome, based on different methods. Table 4 shows the results of GWAS for milk production traits. The GWAS results include the chromosomal position and fraction of variance of 1-Mb genome windows by informative regions (greater than 0.5% or 1.0%). Using BayesGWAS, there were 2,521 regions, with an average number of 20 SNPs, whereas for ssGWAS, there were 2,024 regions with an average number of 20 SNPs.
A total of nine and five significant windows (1-Mb) were identified for MY305 using ssGWAS and BayesGWAS, respectively. The most informative window was detected on chromosome Bos taurus autosomes 15 (BTA15) at 23 Mb using ssGWAS and on BTA14 at 21 Mb using BayesGWAS, which explained 15.73% and 1.0%, respectively. An informative window common to both ssGWAS and BayesGWAS was identified on BTA14 at 1 Mb, which explained 1.54% and 0.79%, respectively. For FY305, we detected 12 significant QTLs using ssGWAS and seven significant QTLs using BayesGWAS. The region of BTA14 at 1 Mb was the most significant 1-Mb window region and a common significant region detected using both methods, which indicated that 11.25% (ssGWAS) and 12.12% (BayesGWAS) of the additive genetic variance was captured, respectively. For PY305, we identified 14 and two significant regions using ssGWAS and BayesGWAS, respectively. Using ssGWASs and BayesGWAS, the most informative window was detected on BTA15 at 24 Mb and on BTA13 at 31 Mb, respectively. A common informative window obtained using both methods was detected on BAT13 at 31 Mb.
The BTA14 region has received considerable attention from many scientists as this region has been reported to harbor a large number of QTLs having an effect on milk production. The diacylglycerol O-acyltransferase 1 (DGAT1) gene located at 1 Mb on BTA14 is generally accepted to be a major gene for milk production [21,22]. In addition to the DGAT1 gene, the 1-Mb region of BTA14 also harbors a number of other genes with linkage to DGAT1, such as cytochrome P450 family 11 subfamily B member 1 [22,23]. Accordingly, using both ssGWASs and BayesGWAS, the 1 Mb region of BTA14 was identified to be a region associated milk and fat yield. Although the 1-Mb region on BTA14 has also previously been shown to be informative with respect to milk protein [21,22], in the present study, we were unable to detect this window with regards to milk protein. This could be attributable to the fact that the collection system for milk protein yield data in Korea was recently changed due to problems associated with the standard solution used. Accordingly, the data for milk protein are not standardized. Therefore, further research is required to obtain uniform milk protein data.
Our findings relating to the 1-Mb region on BTA14, along with other significant regions, are consistent with previously identified regions that have a potential influence on milk production in the Animal QTL database (https://www.animalgenome.org/cgi-bin/QTLdb/BT/index).
Despite the significantly higher level of genetic variance associated with using ssGWAS than when using BayesGWAS, the former was able to identify a larger number of significant regions. Moreover, it is notable that few significant regions were detected using both ssGWAS and BayesGWAS approaches, which can probably be attributed to the differences in methodologies. Methods like Bayes-B are strongly affected by priors, and by the proportion of SNPs assumed not to have an effect (π) [14,15,24]. In contrast to Bayesian methods, ssGWAS analysis is based on available pedigree relationships, and does not depend on deregression [14]. Previous studies have investigated different GWAS approaches using simulated data sets, and found that the different methods were able to detect the same regions [25,26]. In contrast, however, Wang et al [14] found that few common regions were detected using different methods. These disparate findings can probably be explained in terms of the limitations of simulations, which do not capture the complexities of real data.
On the basis of our previous GWAS results, we identified common QTL regions using two different approaches (i.e., ss-GBLUP and Bayes-B). However, we were unable to accurately determine the location and effect size of true QTLs. Therefore, we also compared the accuracy and bias of DGVs when using the two approaches.
Table 5 shows the accuracy and bias of the DGVs deter mined using the ss-GBLUP (single-step method) and Bayes-B (Bayesian method) approaches. To gain estimates of the accuracy and degree of bias of DGVs, we calculated the averages of correlation and regression coefficients in predicting the masking individual in the validation set for analysis of the non-masking individual in the training set, respectively.
The mean accuracies of DGV ss and DGVBayes for MY305, FY305, and PY305 were 0.316±0.018, 0.374±0.070, and 0.354± 0.051, and 0.335±0.034, 0.389±0.052, and 0.357±0.033, respectively. The mean biases of DGVs detected using the single-step method were 1.497±0.210 (MY305), 1.745±0.3266 (FY305), and 1.585±0.203 (PY305), whereas those using the Bayesian method were 1.182±0.262 (MY305), 1.138±0.199 (FY305), and 1.135±0.145 (PY305).
For the three studied traits, we noted small differences in the accuracy of the DGVs obtained using the two methods. The prediction accuracy for trait MY305 (Milk [Acc.]) was lower than that for the other milk production traits (fat and protein). However, compared with Bayes-B, the single-step method for MY305, FY305, and PY305 had a higher bias. By using weighting factors in the Bayes-B method, the more reliably genotyped animals made a greater contribution in estimating SNP marker effects and the prediction of DGVs. We did not apply weighting factors when using ss-GBLUP as real phenotypes were used as response variables when using this method.
A direct comparison of the accuracy and bias of DGV de termined in the present study with those determined previously is difficult given differences in populations and methodologies, such as clustering methodologies (e.g., K-means vs random vs identity by state IBS clustering), the models used, assessments of method accuracy (e.g., genetic correlation vs simple vs variable setting), and other reasons [9]. Furthermore, accuracy depends on various parameters, including the reference population size and its genetic structure [27]. In this regard, in a previous study on Danish Holsteins using a five-fold cross-validation, Su et al [28] reported that the accuracy of DGV (rDGV,EBV) for milk production ranged from 0.64 to 0.70. Similarly, Ding et al [29] in their study of Chinese Holsteins, reported that the accuracy of DGV (rDGV, EBV) in five-fold cross-validation using Bayes-B with priors (π = 0.99) and GBLUP for milk production ranged from 0.317 to 0.380, whereas Luan et al [30] reported an accuracy for milk production of 0.54 to 0.56 in their study on Norwegian red cattle.
We found that the mean accuracies of DGVs for milk pro ductions in the present study were smaller than those obtained previously, which can probably be explained by the fact that the reference population size in our study was smaller than that used in other studies, which was at least 2,000 bulls. Therefore, we intend to increase the size of our reference population by continuously updating data on genotyped animals and phenotypes. This will accordingly improve the accuracy of our genomic predictions. Similarly, if real variants (true QTLs) identified from putative informative regions based on GWAS results can be sequenced in detail, this will enhance the accuracy of genomic prediction.
In this study, we compared the informative regions identified by GWAS and the accuracy of DGV between multiple approaches. We found that different numbers of informative regions were detected when using single-step and Bayesian approaches, and that few common regions were identified by both methods. However, a 1-Mb region on chromosome BTA14, which is known to harbor many genes, was identified by both methods. The mean accuracy of DGVs for milk production traits was similar for both methods, although Bayes-B tended to show a relatively lower bias than the ss-GBLUP method. Therefore, from the perspective of bias, we believe that a Bayesian approach (i.e., Bayes-B) would be more suitable in GS for Korean Holstein populations.
ACKNOWLEDGMENTS
This research was supported by funding from the “Development of selection technology using fetal genomic information” project (no. PJ01199402) of the National Institute of Animal Science, Cheonan, South Korea and 2019 the RDA Fellowship Program of National Institute of Animal Science, Rural Development Administration, Republic of Korea.
Figure 1
Manhattan plots showing genome-wide significant informative windows (≥1% threshold) for adjusted 305-day milk yield (A), adjusted 305-day fat yield (B), and adjusted 305-day protein yield (C) in Korean Holstein cattle using the single-step method.
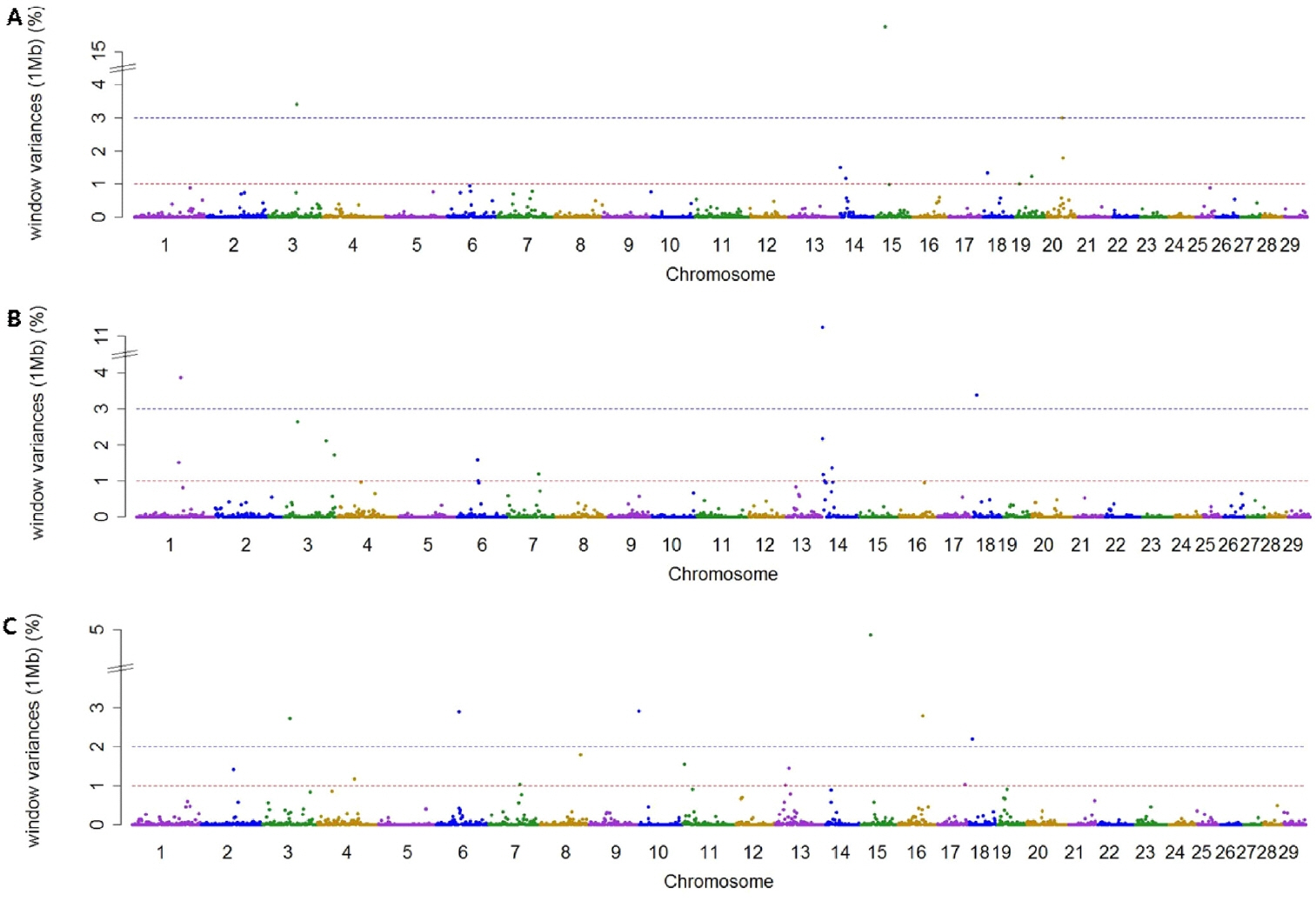
Figure 2
Manhattan plots showing genome-wide significant informative windows (≥0.5% threshold) for adjusted 305-day milk yield (A), adjusted 305-day fat yield (B), and adjusted 305-day protein yield (C) in Korean Holstein cattle using the BayesB method.
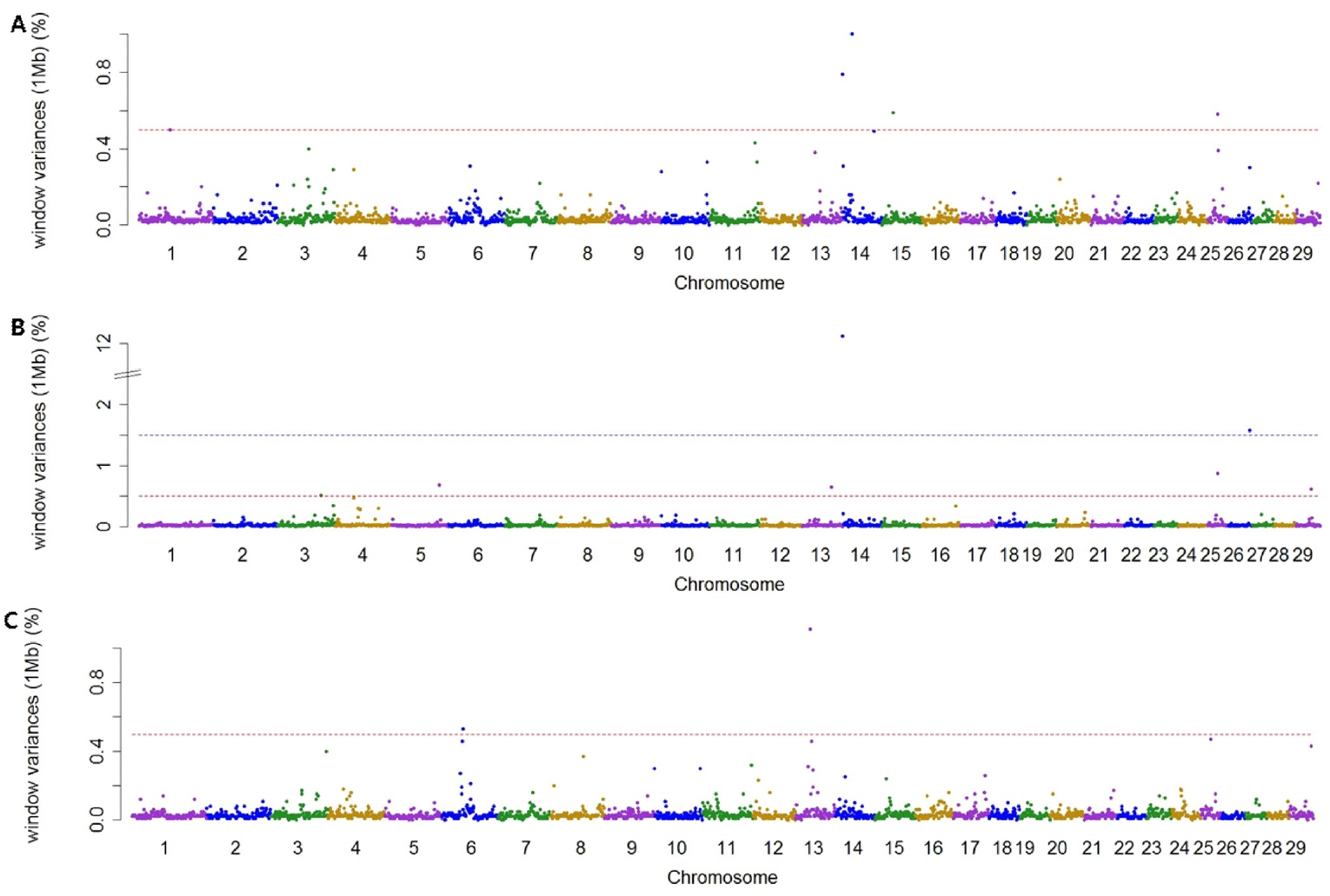
Table 1
Basic statistics of milk composition
| Traits | N | Mean | SD | Min | Max |
|---|---|---|---|---|---|
| MY305 | 265,271 | 8,437.50 | 1,718.70 | 2,504 | 15,962 |
| FY305 | 265,004 | 321.28 | 73.11 | 70 | 600 |
| PY305 | 261,021 | 269.02 | 52.94 | 80 | 500 |
Table 2
Number of masking animals and phenotypes
Table 3
Variance components, standard error, and heritability estimates for milk production in Korean Holstein cattle
| Trait | Additive genetic variance | Residual variance | Heritability |
|---|---|---|---|
| MY305 | 416,220 (±12,855) | 1,204,200 (±10,621) | 0.26 |
| FY305 | 514.23 (±18.79) | 1,947.8 (±15.89) | 0.21 |
| PY305 | 307.44 (±11.20) | 1,102.4 (±9.40) | 0.22 |
Table 4
Result of GWAS for milk production traits
Table 5
Accuracy and bias of DGV in the 5-fold cross-validation using single-step GBLUP and Bayes approach
REFERENCES
1. Weigel K, VanRaden P, Norman H, Grosu H. A 100-year review: methods and impact of genetic selection in dairy cattle—From daughter–dam comparisons to deep learning algorithms. J Dairy Sci 2017; 100:10234–50. https://doi.org/10.3168/jds.2017-12954


2. Meuwissen T, Hayes B, Goddard M. Prediction of total genetic value using genome-wide dense marker maps. Genetics 2001; 157:1819–29.




3. VanRaden PM. Efficient methods to compute genomic predictions. J Dairy Sci 2008; 91:4414–23. https://doi.org/10.3168/jds.2007-0980


4. Kachman SD. Incorporation of marker scores into national genetic evaluations. In : 9th genetic prediction workshop; Kansas City, MO, USA. 2008. p. 92–8.
5. Misztal I, Legarra A, Aguilar I. Computing procedures for genetic evaluation including phenotypic, full pedigree, and genomic information. J Dairy Sci 2009; 92:4648–55. https://doi.org/10.3168/jds.2009-2064


6. Fernando RL, Cheng H, Golden BL, Garrick DJ. Computational strategies for alternative single-step Bayesian regression models with large numbers of genotyped and non-genotyped animals. Genet Sel Evol 2016; 48:96https://doi.org/10.1186/s12711-016-0273-2




7. Fragomeni B, Lourenco D, Tsuruta S, et al. Hot topic: use of genomic recursions in single-step genomic best linear unbiased predictor (BLUP) with a large number of genotypes. J Dairy Sci 2015; 98:4090–4. https://doi.org/10.3168/jds.2014-9125


8. Vitezica Z, Aguilar I, Misztal I, Legarra A. Bias in genomic predictions for populations under selection. Genet Res 2011; 93:357–66. https://doi.org/10.1017/S001667231100022X

9. Lee J, Kachman SD, Spangler ML. The impact of training strategies on the accuracy of genomic predictors in United States Red Angus cattle. J Anim Sci 2017; 95:3406–14. https://doi.org/10.2527/jas.2017.1604


10. Meuwissen T, Hayes B, Goddard M. Genomic selection: A paradigm shift in animal breeding. Anim Front 2016; 6:6–14. https://doi.org/10.2527/af.2016-0002


11. Wiggans GR, Cole JB, Hubbard SM, Sonstegard TS. Genomic selection in dairy cattle: The USDA experience. Annu Rev Anim Biosci 2017; 5:309–27. https://doi.org/10.1146/annurev-animal-021815-111422


12. Sargolzaei M, Chesnais J, Schenkel F. FImpute-An efficient imputation algorithm for dairy cattle populations. J Dairy Sci 2011; 94:421
13. Misztal I, Tsuruta S, Strabel T, Auvray B, Druet T. BLUPF90 family of programs. Athens, GA, USA: University of Georgia; 2007.
14. Wang H, Misztal I, Aguilar I, et al. Genome-wide association mapping including phenotypes from relatives without genotypes in a single-step (ssGWAS) for 6-week body weight in broiler chickens. Front Genet 2014; 5:134https://doi.org/10.3389/fgene.2014.00134



15. Garrick DJ, Taylor JF, Fernando RL. Deregressing estimated breeding values and weighting information for genomic regression analyses. Genet Sel Evol 2009; 41:55https://doi.org/10.1186/1297-9686-41-55




16. Saatchi M, Schnabel RD, Rolf MM, Taylor JF, Garrick DJ. Accuracy of direct genomic breeding values for nationally evaluated traits in US Limousin and Simmental beef cattle. Genet Sel Evol 2012; 44:38https://doi.org/10.1186/1297-9686-44-38



17. Garrick DJ, Fernando RL. Implementing a QTL detection study (GWAS) using genomic prediction methodology. Genome-wide association studies and genomic prediction. Springer; 2013. p. 275–98.

18. Fan B, Onteru SK, Du Z-Q, Garrick DJ, Stalder KJ, Rothschild MF. Genome-wide association study identifies loci for body composition and structural soundness traits in pigs. PloS one 2011; 6:e14726https://doi.org/10.1371/journal.pone.0014726



19. Dematawewa C, Berger P. Genetic and phenotypic parameters for 305-day yield, fertility, and survival in Holsteins. J Dairy Sci 1998; 81:2700–9. https://doi.org/10.3168/jds.S0022-0302(98)75827-8


20. Cho C, Cho K, Choy Y, et al. Estimation of genetic parameters for milk production traits in Holstein dairy cattle. J Anim Sci Technol 2013; 55:7–11. https://doi.org/10.5187/JAST.2013.55.1.7

21. Nayeri S, Sargolzaei M, Abo-Ismail MK, et al. Genome-wide association for milk production and female fertility traits in Canadian dairy Holstein cattle. BMC Genet 2016; 17:75https://doi.org/10.1186/s12863-016-0386-1



22. Jiang L, Liu J, Sun D, et al. Genome wide association studies for milk production traits in Chinese Holstein population. PloS one 2010; 5:e13661https://doi.org/10.1371/journal.pone.0013661



23. Kaupe B, Brandt H, Prinzenberg E, Erhardt G. Joint analysis of the influence of CYP11B1 and DGAT1 genetic variation on milk production, somatic cell score, conformation, reproduction, and productive lifespan in German Holstein cattle. J Anim Sci 2007; 85:11–21. https://doi.org/10.2527/jas.2005-753



24. Van Hulzen K, Schopen G, van Arendonk J, et al. Genome-wide association study to identify chromosomal regions associated with antibody response to Mycobacterium avium subspecies paratuberculosis in milk of Dutch Holstein-Friesians. J Dairy Sci 2012; 95:2740–8. https://doi.org/10.3168/jds.2011-5005


25. Zeng J, Pszczola M, Wolc A, et al. Genomic breeding value prediction and QTL mapping of QTLMAS2011 data using Bayesian and GBLUP methods. BMC Proc 2012; 6:Suppl 2S7




26. Wang H, Misztal I, Aguilar I, Legarra A, Muir W. Genome-wide association mapping including phenotypes from relatives without genotypes. Genet Res 2012; 94:73–83. https://doi.org/10.1017/S0016672312000274

27. Lee SH, Clark S, van der Werf JH. Estimation of genomic prediction accuracy from reference populations with varying degrees of relationship. PloS one 2017; 12:e0189775https://doi.org/10.1371/journal.pone.0189775



28. Su G, Guldbrandtsen B, Gregersen V, Lund M. Preliminary investigation on reliability of genomic estimated breeding values in the Danish Holstein population. J Dairy Sci 2010; 93:1175–83. https://doi.org/10.3168/jds.2009-2192


29. Ding X, Zhang Z, Li X, et al. Accuracy of genomic prediction for milk production traits in the Chinese Holstein population using a reference population consisting of cows. J Dairy Sci 2013; 96:5315–23. https://doi.org/10.3168/jds.2012-6194


30. Luan T, Woolliams JA, Lien S, Kent M, Svendsen M, Meuwissen TH. The accuracy of genomic selection in Norwegian red cattle assessed by cross validation. Genetics 2009; 183:1119–26. https://doi.org/10.1534/genetics.109.107391



- TOOLS
-
METRICS

- Related articles
-
Genome-wide association research on the reproductive traits of Qianhua Mutton Merino sheep






 PDF Links
PDF Links PubReader
PubReader ePub Link
ePub Link Full text via DOI
Full text via DOI Full text via PMC
Full text via PMC Download Citation
Download Citation Print
Print




