 |
 |
| Anim Biosci > Volume 30(9); 2017 > Article |
|
Abstract
Objective
Calving ease (CE) is a complex reproductive trait of economic importance in dairy cattle. This study was aimed to investigate the genetic merits of CE for Holsteins in Korea.
Methods
A total of 297,614 field records of CE, from 2000 to 2015, from first parity Holstein heifers were recorded initially. After necessary data pruning such as age at first calving (18 to 42 mo), gestation length, and presence of sire information, final datasets for CE consisted of 147,526 and 132,080 records for service sire calving ease (SCE) and daughter calving ease (DCE) evaluations, respectively. The CE categories were ordered and scores ranged from CE1 to CE5 (CE1, easy; CE2, slight assistance; CE3, moderate assistance; CE4, difficult calving; CE5, extreme difficulty calving). A linear transformation of CE score was obtained on each category using Snell procedure, and a scaling factor was applied to attain the spread between 0 (CE5) and 100% (CE1). A sire-maternal grandsire model analysis was performed using ASREML 3.0 software package.
Results
The estimated direct heritability (h2) from SCE and DCE evaluations were 0.11±0.01 and 0.08±0.01, respectively. Maternal h2 estimates were 0.05±0.02 and 0.04±0.01 from SCE and DCE approaches, respectively. Estimates of genetic correlations between direct and maternal genetic components were −0.68±0.09 (SCE) and −0.71±0.09 (DCE). The average direct genetic effect increased over time, whereas average maternal effect was low and consistent. The estimated direct predicted transmitting ability (PTA) was desirable and increasing over time, but the maternal PTA was undesirable and decreasing.
Conclusion
The evidence on sufficient genetic variances in this study could reflect a possible selection improvement over time regarding ease of calving. It is expected that the estimated genetic parameters could be a valuable resource to formulate sire selection and breeding plans which would be directed towards the reduction of calving difficulty in Korean Holsteins.
Calving ease (CE), also termed as dystocia, is a complex reproductive trait of economic importance in the dairy industry [1], especially in primiparous cows, that directly influences the profitability of herds and animal welfare [2]. It concerns, according to Meijering [3], not only the short-term farm profits through the loss of calf, death of dam, veterinary fees, and extra labors, but also the long-term animal performances i.e. health issues, and fertility problems, reduced production, and involuntary culling. Although, a better herd management (heifer rearing, feeding during gestation) could improve calving difficulty, many other studies, alongside Dekkers [1], suggest that the selection and a proper breeding approach targeting better CE might be a better choice in the long term.
The CE at parturition, from the biological perspective, is mainly influenced by the calf size and pelvic dimension of a dam [3]. For this reason, calving performance is often considered to be consisted of both direct and maternal genetic components (Figure 1). A direct genetic component indicates the ability of a calf to be born easily, whereas a maternal genetic component explains the ability of the cow to give birth easily [4]. The relationship between these genetic components also becomes important, as it might contribute a role in the estimation of genetic parameters for the trait, and thus influencing their responses to selection. Evidences for adequate variances in both genetic components, indicating an effective selection of the trait, were already reported in various populations [2].
Typically, the analysis of CE is not so straight forward due to its nature of expression, which is an ordered discrete variable. Genetic studies on CE as reported previously were either based on linear models [5,6] or threshold models [7,8]. Some studies also performed a linear transformation of the trait levels by means of Snell scores [9], before fitting a linear model with CE [10]. Although, threshold model is often chosen for its better fit to a categorical trait [11], there are some situations, such as the relatively smaller sizes of the contemporary and the sire group, where a linear model analysis could perform better than the former model [12].
Although a positive trend in production traits has been achieved, there is a growing concern for the reproductive performance of the dams, in particular to calving events leading to economic losses in the farm. Significant selection strategies are yet to be deployed to the local stock to ensure calving improvement. Therefore, given no previous attempts on realizing CE properly, obtaining an adequate knowledge on the genetic merits of this trait is crucial. This study, being the first attempt in Korean Holstein population, was essentially aimed to unveil the true genetic merit of CE from different genetic standpoints lying underneath the phenotypic scores.
This study included field records on calving from Holstein heifers (first calving cows) that calved between 1993 and 2015. A total of 297,614 field-based CE records were collected, and all records were scored into five ordered categories of birth events, from an easier calving (CE1) to the maximum difficulty calving (CE5), based on the magnitude of the difficulties faced during the births of the calves and a relative assistance required by their dams. These allocated CE scores ranged from 1 through 5, representing an easy calving (non-assisted), slight assistance calving (1 person), moderate assistance calving (2 to 3 persons), a difficult calving (4 or more persons), and an extreme difficulty calving (surgical assistance), respectively. Homogeneity of the data was attempted through restrictions on the gestation period and age at first calving of the cows, which were 240 to 296 d and 18 to 42 mo, respectively. It was also checked that each calf with a CE score (in the phenotype dataset) also had both parents known, and was discarded otherwise. Although a lack of dam information was not allowed, a missing maternal-grandsire information was ignored from data exclusion criteria. Lastly, a linear transformation using [9] the Snell procedure was performed on the discrete CE scores (with a skewed distribution).
Ideally, the Snell procedure considers an underlying continu ous distribution of the trait. This helps to attain a better normal distribution which is also an important requirement for any linear analysis. A basic assumption for Snell score is such that there lies a latent continuous scale between interval of ordered categories, and each transformed score represents the middle of the interval. To compute scores, an approximation procedure is applied through a logistic model that could be generalized for a normal distribution. Thus, an approximated solution to a pair of boundary points is estimated by substituting the observed proportion as the theoretical proportion into the derivatives of the log likelihood. These values are calculated from weighted sums of the proportions (weighted by the number of observations). In general, if we consider i = 1, 2 …, m groups of observations and j = 1, 2 …, k categories of calving difficulty, the derived estimation equations [9] are as follows:
for j = 2, 3 …, (k-2);
for j = (k-1);
where is X̂j the estimated boundary points for calving difficulty category j; Pij is the observed probability of sex of calf i in calving difficulty category j; nij is the frequency of scale values in sex of calf i of calving difficulty category j; Nj is the sum of observations in calving difficulty category j.
These two equations provided estimates for the intervals of (X̂3 – X̂2), (X̂2 – X̂1), …, (X̂k-2 – X̂k-1). Once an arbitrary value of 0 was set to the first boundary point, subsequent boundary points for other categories was calculated by adding the previous category estimates. For the two extreme categories, scores are derived from the corresponding expected values under the two tails of the distribution. The scores for the first and last category are given by x̂2 + (logeP1/Q1) and x̂k-1 + (logePk–1/Qk–1) where P1 is the probability of a value greater than x1 and Q1 is the 1–P1, and Pk–1 is the probability of a value less than xk–1 and Qk–1 is the 1–Pk–1. The Snell transformed CE scores for sex groups were computed following the above steps. Then, the derived score range of calving difficulty was forced to a scale spanning 0% to 100%, such that a score of 0% expressed the least of CE (an extreme difficulty calving) and 100% denoted the greatest of CE (a normal calving).
Pedigrees for animals (progeny or dams) with phenotypes were prepared following the sire-maternal grandsire (S-MGS) architecture. Thus, two distinct set of files (pedigree and phenotype) were prepared for two different analysis approaches, namely the service sire calving ease (SCE) and daughter calving ease (DCE). Details of pedigree structure and phenotypic data are provided in Table 1.
The SCE and DCE approach accounted the relationship between a progeny to its sire and a first-calving daughter to its sire, respectively, given the same CE record in perspective. The dataset for SCE based analysis was comprised of 147,526 CE records, whereas for DCE approach, it retained at 132,080 records after discarding CEs of the daughters with no sire records. Sex of the calf born and the age at first-calving of its dam in each calving event were fitted as fixed effects with the response variable. However, the herd-year-season (HYS) class, created by merging herd number, calving years and calving seasons, was fitted as a random effect. Note that four calving seasons were considered likewise, the summer (September to November), winter (December to February), autumn (March to May), and spring (June to August). Both sire and maternal grandsires were treated random in the model as well. The variances of parameters and covariances between random genetic components were estimated using the ASREML 3.0 software package [13] which implements a restricted maximum likelihood approach. The genetic model applied for estimating sire additive genetic, maternal effects and residual variances in matrix notation was
where Y is the vector of Snell transformed CE scores on a 0 to 100 scale; b is the vector of fixed age at calving effect (in months); h is the vector of random HYS effect; s is the vector of random sire effect; mgs is the vector of random MGS effect; and e is the vector of random residual effect. X, W, Z1, and Z2 were incidence matrices relating the effects to phenotypes. Relationships among bulls were ignored for both sire and MGS effects.
The HYS effect was random because convergence problems can occur when all records in a fixed environment group belong to an extreme category [14]. As seen in this study, more than 67% of the records included a CE score of 1 across all sample data sets. The estimation of correlation between sire and MGS effects were allowed by the model through inclusion of bulls as both sires and MGSs, even if one or more bulls had observations for only one effects (i.e., either found as a sire or a MGS).
Sire (
σ s 2 σ m g s 2
Where
σ D 2 σ M 2 σ p 2 = σ s 2 + σ mgs 2 + σ s , mgs + σ hys 2 + σ e 2 h D 2 = σ D 2 / σ P 2 h M 2 = σ M 2 / σ P 2
Firstly, the average solutions of direct and maternal effects were evaluated by year of calving to explain how the additive genetic effect might have contributed to the animal phenotype (trend). For each record, the direct and maternal effect were calculated by ŝsire and m̂mgs – 0.5ŝmgs, respectively, where ŝ is the sire and MGS solutions for the sire and m̂ is the solution for the MGS of the progeny or first-calving daughter. Secondly, the additive genetic trends of direct and maternal predicted transmitting ability (PTA) for the sires were also evaluated and plotted according to their birth years. The direct PTA (dPTA) was equivalent to the estimated solution for bull as sire (ŝ). The maternal PTA (mPTA) was derived from m̂ – 0.5ŝ, where m̂ is the solution for the bull as MGS.
Distribution of calving ease scores by sex of calves are presented in Table 2. Irrespective of datasets, Holstein sires produced calves with fewer difficult births. An overall 79% of calving reports showed easier calving event. Thus, a ratio of 1:680 was observed for difficult calving (CE≥4) to the easy calving (CE1) in the larger data set. This study clearly indicates that Korean Holstein heifers are largely easy calvers. Similar evidences of Holstein cattle being naturally easy calvers were reported earlier [16]. A report on first parity Charolais heifers [10] also deemed consistent (72% easy calving) with the present study. Among the difficult births reported across parities in Brown Swiss and Jersey cows [17], most of them were reported in the first parity heifers; and then, there was a greater difference between the proportion of first and second parity difficult births than the differences between second and later parities. Although the present study considered first parity CE records only, a further investigation into the later parity records in our stored database (results not shown) approved such consistencies with other reports too.
Presented in Table 3 are the (co)variances of direct and maternal contributions for CE, estimated through the SCE and DCE method based S-MGS models. The heritability (h2) estimates for direct and maternal components from SCE based model were 0.11± 0.01 and 0.06±0.02, respectively. The daughter CE method, however, estimated a little lower h2 for direct genetic effect (0.08±0.01) and maternal genetic effect (0.04±0.01). These overall differences in estimates were expected. The genetic variances due to direct and maternal effects were somewhat similar. The existence of direct genetic variances indicated the possibilities for selection responses towards a reduced calving difficulty, through a relative reduction of calf-size in relation to the dam’s pelvic openings. The correlation estimates between direct and maternal components were negative across models such as, −0.68±0.09 (SCE) and −0.71± 0.09 (DCE), possibly because of the negative covariances between them as it is commonly reflected by the relationships between calf size and dam’s pelvic dimension.
The work of Eaglen and Bijma [18] showed very similar heri tability estimates (direct h2, 0.08; maternal h2, 0.04) in Dutch Holstein-Friesian cattle. The authors in a 2009 study [10], who also followed the Snell transformation of CE records and a linear model fit, reported very similar direct h2 (0.14) and maternal h2 (0.06) for calving ease in Charolais cattle. Likewise, a greater agreement was established with other studies irrespective of their choices for models of parameters estimations [5,15,16,19,20]. Despite the consistency for direct h2 of CE from Heringstad et al [21], their h2 estimate of maternal component was slightly higher (0.09). Some linear model studies [6,22], however, showed a trend where the linear models estimates were generally lower than those of the threshold models reports. To assert the differences between SCE and DCE model estimates in this study, a report by Weigel [23] greatly supported the present outcomes too.
The presence of antagonistic genetic relationships, to a varying magnitude, between direct and maternal effects (rGDM) for calving ease was generally reported by others as well. A substantial harmony with similar estimates between these components was also reported by Mujibi and Crews [10]. In Canadian Holstein [22], a negative correlation between these genetic effects for CE (−0.16) was found as well. Similarly but within a slightly wider range (−0.04 to −0.44), some negative direct-maternal genetic correlations from animal and S-MGS models were also reported in Dutch Holstein Friesian cattle [18]. They evidently agreed, based on the outcome differences among the data subsets, that an accurate estimation of rGDM was rather difficult, even with about 100,000 records. Likewise, a fairly closer range of −0.08 to −0.47 in other dairy cattle studies was not unexpected [15,16]. In contrast, the study in Swedish Holstein [20] disagreed slightly by their weak positive or negative correlations, respectively, in calving difficulty trait. The magnitude at which reports differed might be attributed to the breed and population differences, in addition to the models of estimations. In support of the fact, an earlier work in 1996 [24] stated that estimates in beef cattle often tend to be more negative. The study of Mujibi and Crews [10], in support with Phocas and Sapa [25], illustrated that CE direct and maternal effects, that are genetically correlated in a negative way, could necessarily indicate the influences of physiological and biological factors of the heifer such as the size of pelvic opening at calf-birth. The work of Phocas and Sapa [25] treated CE as a trait of the dam.
The calving ease trends in the first parity heifers, Figure 2, showed that there was relatively larger proportion of difficult births reports (i.e., CE category ≥2) at the earlier stages of the study. Over the years, with the increased yearly reporting, there was a gradual decline in difficult calving (>CE2), which is largely agreeable with trends shown by Hansen et al [26]. In contrast, a 2007 study [21] in Norwegian Red cows noticed an increasing yearly trend in the incidence of slight problem to difficult calving, in particular to the primiparous cows with greater calving problems than the older cows. Figure 3 also confirmed that female progenies calved somewhat easily over the period, and it was a commonly agreeable fact with previous reports including Dhakal et al [27]. Also, the proportions of animals, irrespective of sexes, with a greater calving ease fairly increased over the years. This was deemed somewhat unlikely as the calf sizes at birth increased in recent years, which might be due to the use of semen from superior foreign sires. It is assumed from the study, given no evidence of selection for CE trait yet exists in Korean Holsteins, that there might be some possible indirect selection responses benefiting the birth events in the local population, as passed through the superior genetics of the foreign Holstein bulls. This improved performance could also indicate the practice of better animal care and management system by the farmers in recent years, yet this would not be feasible in a long-term basis.
The additive genetic trends in the progeny or first calving daughters are shown as average additive genetic solution per calving-year in Figure 4 for SCE and DCE methods, respectively. For SCE, the increases in the direct and average genetic components of CE from progenies were gradual. Some inconsistencies in these components, however, from DCE based estimates were observed for some initial years of the study which later showed more consistency. Contrarily, the average maternal effect somehow remained consistent and higher than the average genetic effects until 2009. Although, the differences in estimates among methods were slightly unclear due to the nature of the data, in an overall term, both the direct genetic and total average effect showed a greater progress in attainment of easier calving events in the studied population, and it deemed greatly favorable if selection decisions are to be made on this trait. There remains a concern, however, for the consistent and unchanged overall maternal contributions, in which an increment is desired. Mujibi and Crews [10] showed significant genetic trends for the direct effects of CE in Charolais cattle, whereas no trend for maternal effects was shown. The estimates from SCE and DCE slightly differed from each other, which was deemed higher for the later method. It is to be noted that the estimates based on SCE approach, other than the daughter CE, generally play a greater role in selection of sires as the direct components from SCE has a higher heritability and a direct genetic relationship to the progenies under consideration.
The estimates on sire or artificial insemination (AI) bull aver ages for direct and maternal PTA were plotted according to their birth-year (Figure 5). The averages on sires dPTA showed a significant change occurred between 1998 and 2003, which illustrates the shift from a negative contribution of sires on the normal calving ease to a desirable positive effect. Although, sire’s dPTA changes since then were not consistent, they remained positive, indicating the sire’s direct contribution to the progenies or daughters to ease the calving event, in a general perspective. In contrast, the trend for mPTA of the AI bulls, which degraded inconsistently, irrespective to SCE or DCE, also indicates their negative contributions to the desired calving events. Nonetheless, the mPTA estimate (maternal estimation of breeding value [EBV]) from DCE method was noticeably lower than that from the SCE method estimate. This might indicate that superior genetics, either foreign bulls or progenies from selection programs, that were introduced in the local population might have not concerned for maternal genetic contributions.
In overall, the outcomes in this study feature some important aspects which should be considered for the genetic evaluation of local Holsteins. Although some genetic progresses on calving difficulty possibly had occurred through exotic germplasms, yet they are evidently very low as compared to other foreign populations, and rather somewhat inconsistent. Sires with degrading mPTA and high antagonistically related maternal and direct genetic components further emphasizes the consideration for existing calf sizes and pelvic dimension of the dams at birth in the Korean Holsteins. However, the exploitation of genetic variance which exists in the population could bring benefits through selection.
Linear models have been routinely used to evaluate categorical traits (CE and still birth) or categorical traits in association with other quantitative traits (body weight, calving ease, calving interval, and weaning weight) [28,29]. The 2009 study [10] also reported a multivariate linear animal model approach after Snell transformation. As it appeared, linear models considering an underlying scale for categorical traits were deemed to underestimate the parameters compared with threshold models [20]. In so far as the EBV or estimation of progeny differences using field data is concerned, there are relatively small comparative advantages of threshold models over linear models [12,30], and both models tend to rank animals mostly in the same manner [19]. In practice, however, it was found somewhat difficult to directly compare the current estimates of calving ease scores with other published reports. This is because many countries tend to adopt a certain definition of the trait as well as its method of evaluation based on their breeding goal and available resources.
Calving ease, in this study, was defined from both progeny and dam perspectives. According to Weigel [23], SCE reflects the tendency of calves from a particular service sire to be born more easily (or more difficult) than an average calf, whereas a DCE illustrates the tendency of daughters of a particular sire to have more (or fewer) problems at calving time than an average cow and to produce calves that are born more easily (or more difficult) than calves produced by an average cow. Eventually, as he mentioned further, heritability estimates from SCE approach results slightly higher values than DCE. Thus, service SCE helps greatly in selection of safer bulls as mating partners with primiparous heifers. The DCE, in contrast, could be used as assistance to SCE, as a secondary tool for selection of sires. It is to be noted that this study was focused on investigating the different genetic components that are contributed from different genetic sources, but not necessarily on comparing the performances of the approaches.
This study investigated CE genetic components through ser vice sire and DCE approaches. In so far as much as the genetic merit is concerned, heritability estimates for direct and maternal genetic components for CE in the study were mostly lower. The direct heritability estimates were higher than maternal h2 estimates. The antagonistic correlation estimates between direct and maternal genetic components were also deemed high and indicated that there could be roles from maternal factors such as pelvic dimensions. However, evidence on sufficient genetic variances could reflect a selection improvement over time on CE. It is realized that direct genetic contributions resulting easier calving increased over time, whereas in overall, the maternal component was consistent and relatively low. A straightforward evidence of undesired and deteriorating maternal contributions on sires (sire EBV) were observed from the dams of sires, even though direct contributions were as desired. These outcomes were consistent with previous reports too. Thus, these results could be a good starting point for the development of selection and breeding plans for calving ease in the local Holstein population. A detailed future analysis with this trait alongside still-birth and birth weight of calves would validate present estimates with greater accuracies.
ACKNOWLEDGMENTS
This research was supported by the funding from the project “National level improvement of dairy cattle selection system using genomic platform (Project No: PJ01260603)” and the “RDA Research Associate Fellowship Program” of the National Institute of Animal Science, Cheonan, Korea.
Figure 1
Direct and maternal genetic influences on calving ease (dystocia) [4]. GM and GD correspond to the maternal and direct genetic components for calving ease; EM and ED correspond to the maternal and direct environmental components for calving ease; rDM is the genetic correlation between and maternal effects for calving ease.
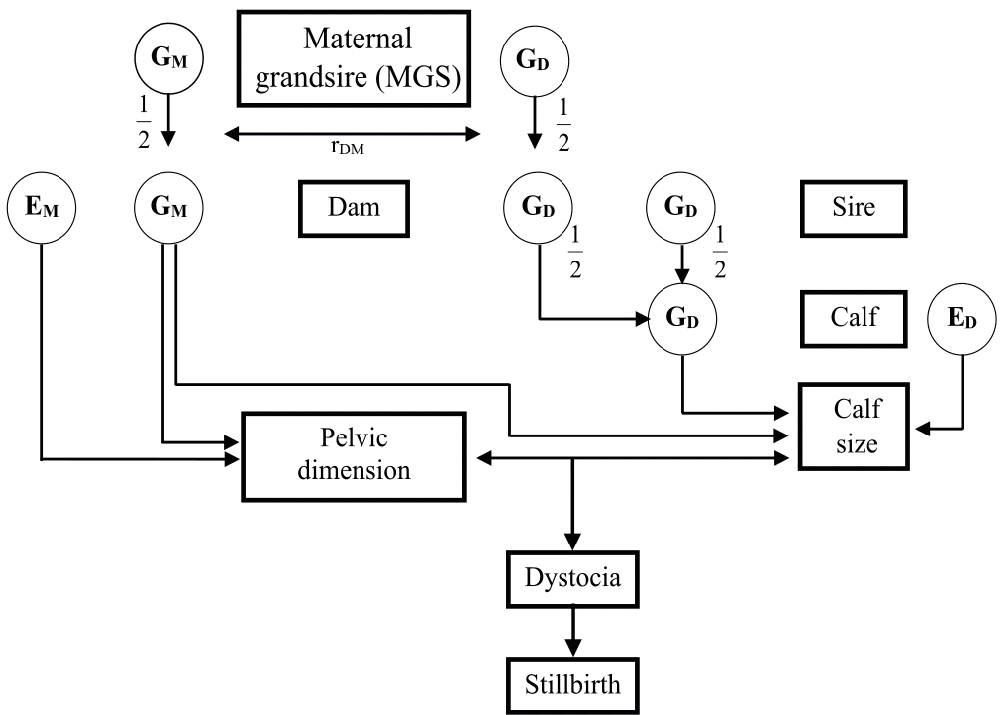
Figure 2
Proportions of calving ease (CE) categories (normal [■/□], moderate [▲/△], and difficult [●/○]) in Holstein cattle using service sire CE (continuous line) and daughter CE (dashed line) models.

Figure 3
Proportions of calving ease categories (top; normal [■/□], moderate [▲/△], and difficult [●/○]) and average Snell scores of calving ease (CE, bottom) according to sex of Holstein calves in the service-sire CE (SCE, left) and daughter CE (DCE, right) datasets. Males and females in the figures are indicated by open and filled symbols, respectively.
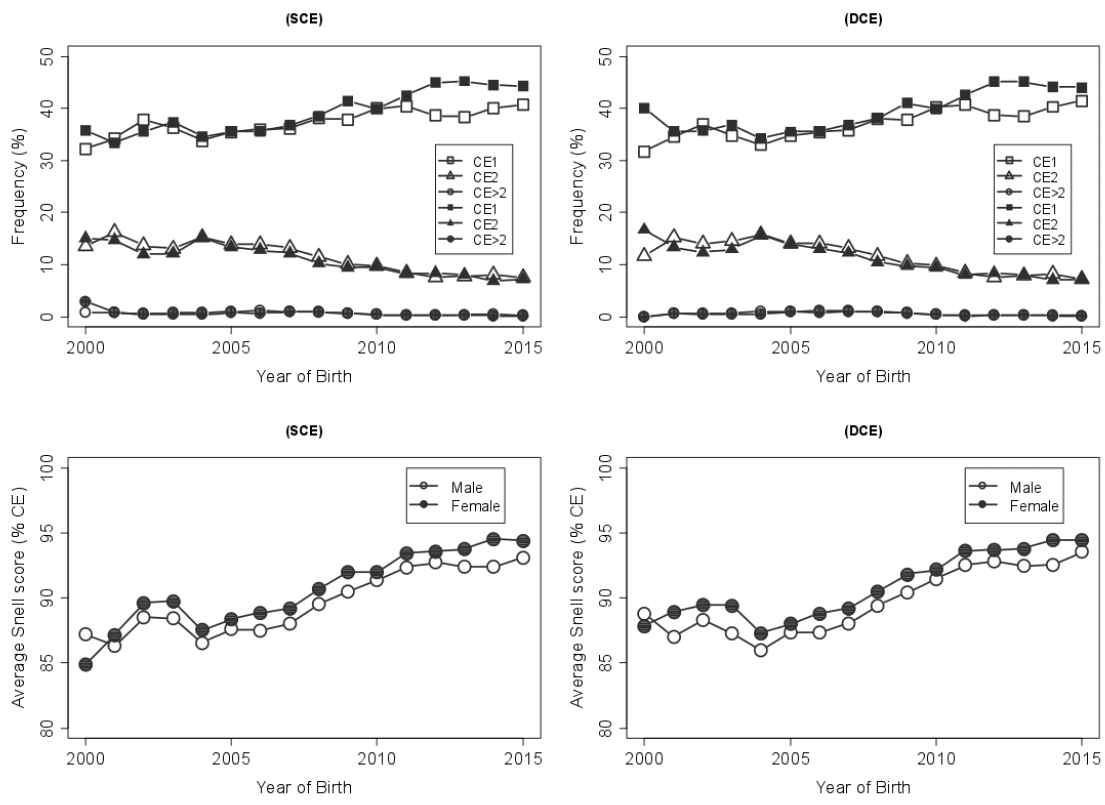
Figure 4
Estimates of average direct (DIR [■/□]), maternal grandsire (MGS [▲/△], and total (TOT [●/○]) genetic effects in Holstein cattle using service sire calving ease (CE, continuous line) and daughter CE (dashed line) models.
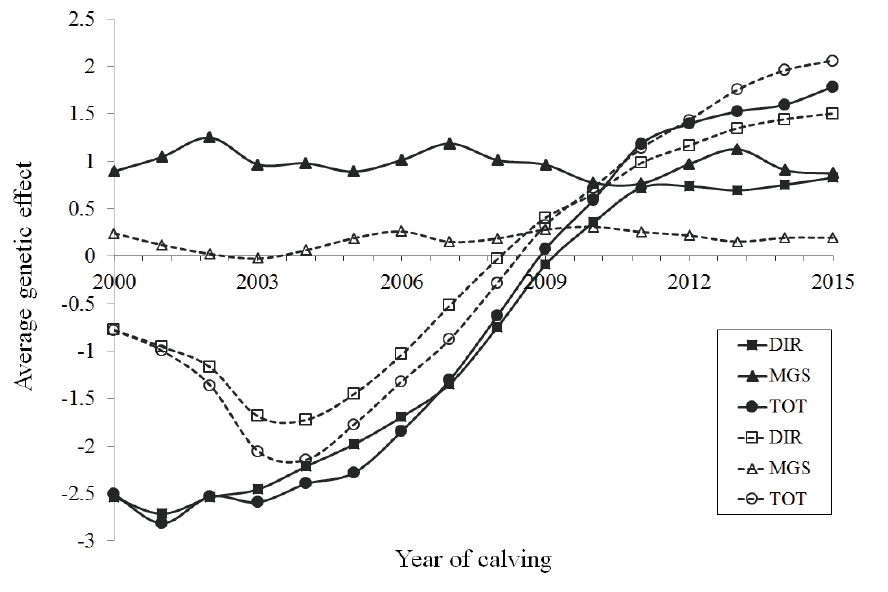
Figure 5
Estimates of average direct and maternal predicted transmitting ability (dPTA [■/□] and mPTA [▲/△]) of Holsten sires for calving ease by their year of birth from service sire calving ease (CE, continuous line) and daughter CE (dashed line) models.
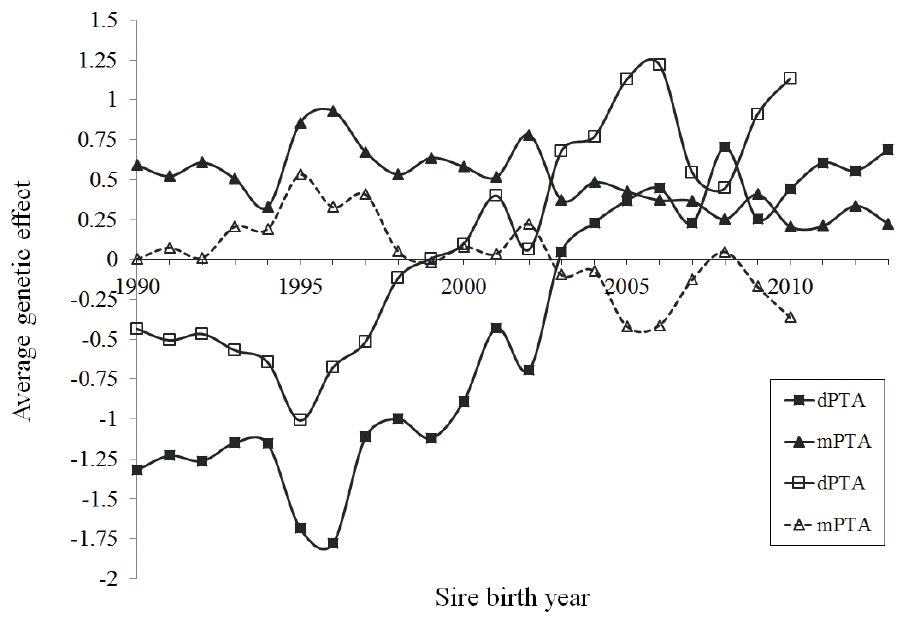
Table 1
Description of pedigree structure and phenotype data for service sire calving ease (SCE) and daughter calving ease (DCE) methods
| Items | SCE | DCE |
|---|---|---|
| Pedigree structure1) | ||
| Number of animals | 4,666 | 5,059 |
| Number of sires | 763 | 838 |
| Number of dams | 2,989 | 3,185 |
| Number of inbred | 2,366 | 2,331 |
| Number of animals with both parents known | 3,590 | 3,769 |
| Longest ancestral path (LAP) | 17 | 16 |
| Inbreeding coefficient (average) | 0.0144 | 0.0125 |
| Inbreeding coefficient (minimum) | 1.91E-05 | 1.91E-05 |
| Inbreeding coefficient (maximum) | 0.25 | 0.25 |
| Phenotype dataset2) | ||
| Number of records | 147,526 | 132,079 |
| Number of bulls | 1,212 | 1,192 |
| Number of MGS | 261 | 264 |
| Number of contemporary group (HYS) | 61,696 | 55,814 |
| Age at first calving (in months) | 18–42 | |
Table 2
Percent observations of calving ease (CE) categories and corresponding Snell scores (% unassisted calving, in parenthesis) according to sex of calves
| Dataset | Sex of calf | Calving ease score1) | ||||
|---|---|---|---|---|---|---|
|
|
||||||
| 1 | 2 | 3 | 4 | 5 | ||
| Service sire CE | Male | 38.30 (99.22) | 10.10 (61.61) | 0.49 (32.78) | 0.04 (15.74) | 0.02 (0) |
| Female | 40.99 (100) | 9.62 (60.77) | 0.38 (32.26) | 0.02 (19.01) | 0.04 (5.90) | |
| Total | 79.29 | 19.72 | 0.87 | 0.06 | 0.06 | |
| Daughter CE | Male | 38.38 (99.25) | 10.03 (61.79) | 0.48 (32.93) | 0.03 (15.74) | 0.02 (0) |
| Female | 41.05 (100) | 9.57 (61.11) | 0.38 (32.74) | 0.02 (19.55) | 0.04 (6.65) | |
| Total | 79.43 | 19.60 | 0.86 | 0.05 | 0.06 | |
Table 3
Estimates of genetic parameters for calving ease of Korean Holsteins using sire-maternal grandsire (S-MGS) model in the first parity
REFERENCES
2. Carnier P, Albera A, Dal Zotto R, et al. Genetic parameters for direct and maternal calving ability over parities in Piedmontese cattle. J Anim Sci 2000; 78:2532–9.


3. Meijering A. Dystocia and stillbirth in cattle a review of causes, relations and implications. Livest Prod Sci 1984; 11:143–77.

4. Meijering A. Dystocia in dairy cattle breeding with special attention to sire evaluation for categorical traits [PhD thesis]. Wageningen, The Netherlands: Wageningen Agricultural University; 1986.
5. Eriksson S, Näisholm A, Johansson K, Philipsson J. Genetic parameters for calving difficulty, stillbirth, and birth weight for Hereford and Charolais at first and later parities. J Anim Sci 2004; 82:375–83.


6. Jamrozik J, Fatehi J, Kistemaker GJ, Schaeffer LR. Estimates of genetic parameters for Canadian Holstein female reproduction traits. J Dairy Sci 2005; 88:2199–208.


7. López de Maturana E, Ugarte E, Komen J, van Arendonk JAM. Consequences of selection for yield traits on calving ease performance. J Dairy Sci 2007; 90:2497–505.


8. Wiggans GR, Cole JB, Thornton LLM. Multiparity evaluation of calving ease and stillbirth with separate genetic effects by parity. J Dairy Sci 2008; 91:3173–8.


10. Mujibi FDN, Crews DH. Genetic parameters for calving ease, gestation length, and birth weight in Charolais cattle. J Anim Sci 2009; 87:2759–66.


12. Phocas F, Laloë D. Evaluation models and genetic parameters for calving difficulty in beef cattle. J Anim Sci 2003; 81:933–8.


13. Gilmour AR, Gogel BJ, Cullis BR, Thompson R. ASReml user guide release 3.0 [Internet]. Hemel Hempstead, HP1, 1ES, UK: VSN International Ltd; c2008. [cited 2017 Mar 30]. Available from: www.vsni.co.uk
14. Misztal I, Gianola D, Foulley JL. Computing aspects of a nonlinear method of sire evaluation for categorical data. J Dairy Sci 1989; 72:1557–68.

15. Wiggans GR, Misztal I, Van Tassell CP. Calving ease (Co)variance components for a sire-maternal grandsire threshold model. J Dairy Sci 2003; 86:1845–8.


16. Hickey JM, Keane MG, Kenny DA, et al. Heterogeneity of genetic parameters for calving difficulty in Holstein Heifers in Ireland. J Dairy Sci 2007; 90:3900–8.


17. Cole JB, Goodling RC, Wiggans GR, Vanraden PM. Genetic evaluation of calving ease for Brown Swiss and Jersey bulls from purebred and crossbred calvings. J Dairy Sci 2005; 88:1529–39.


18. Eaglen SA, Bijma P. Genetic parameters of direct and maternal effects for calving ease in Dutch Holstein-Friesian cattle. J Dairy Sci 2009; 92:2229–37.


19. Weller JI, Ron M. Genetic analysis of fertility traits in Israeli Holsteins by linear and threshold models. J Dairy Sci 1992; 75:2541–8.


20. Steinbock L, Näsholm A, Berglund B, Johansson K, Philipsson J. Genetic effects on stillbirth and calving difficulty in Swedish Holsteins at first and second calving. J Dairy Sci 2003; 86:2228–35.


21. Heringstad B, Chang YM, Svendsen M, Gianola D. Genetic analysis of calving difficulty and stillbirth in Norwegian red cows. J Dairy Sci 2007; 90:3500–7.


22. Luo MF, Boettcher PJ, Dekkers JCM, Schaeffer LR. Bayesian analysis for estimation of genetic parameters of calving ease and stillbirth for Canadian Holsteins. J Dairy Sci 1999; 82:1848–58.

23. Weigel K. Daughter and service sire calving ease-there’s new help to avoid calving ease problems [Internet]. Breeders Journal; c2002. [cited 2017 Mar 30]. Available from: http://usa.absglobal.com/tech_serv/resources/resourcefiles/dairy/CalvingEasearticle.pdf
24. Robinson DL. Models which might explain negative correlations between direct and maternal genetic effects. Livest Prod Sci 1996; 45:111–22.

25. Phocas F, Sapa J. Genetic parameters for growth, reproductive performance, calving ease and suckling performance in beef cattle heifers. J Anim Sci 2004; 79:41–8.

26. Hansen M, Misztal I, Lund MS, Pedersen J, Christensen LG. Undesired phenotypic and genetic trend for stillbirth in Danish Holsteins. J Dairy Sci 2004; 87:1477–86.


27. Dhakal K, Maltecca C, Cassady JP, et al. Calf birth weight, gestation length, calving ease, and neonatal calf mortality in Holstein, Jersey, and crossbred cows in a pasture system. J Dairy Sci 2013; 96:690–8.


28. Cole JB, Wiggans GR, VanRaden PM, Miller RH. Stillbirth (co)variance components for a sire-maternal grandsire threshold model and development of a calving ability index for sire selection. J Dairy Sci 2007; 90:2489–96.


- TOOLS
-
METRICS

- Related articles
-
Genetic parameter analysis of reproductive traits in Large White pigs2022 November;35(11)





 PDF Links
PDF Links PubReader
PubReader ePub Link
ePub Link Full text via DOI
Full text via DOI Full text via PMC
Full text via PMC Download Citation
Download Citation Print
Print




